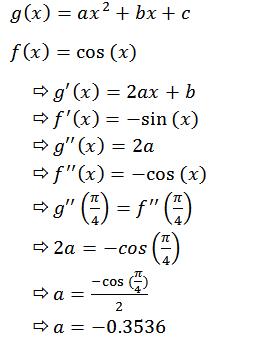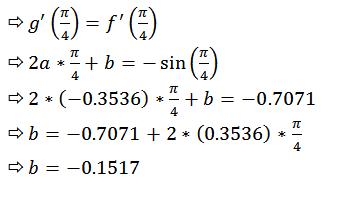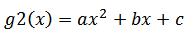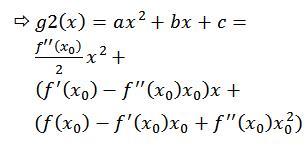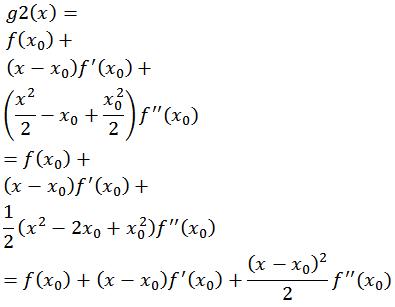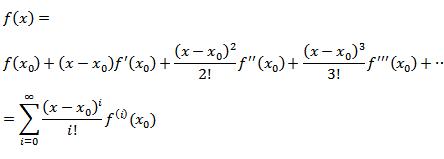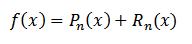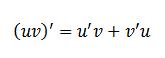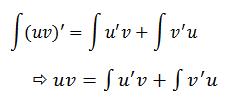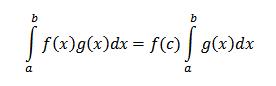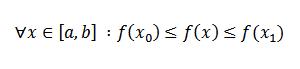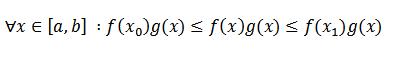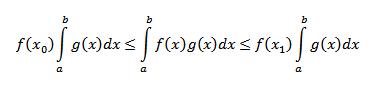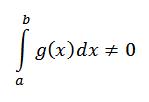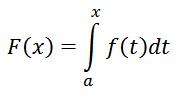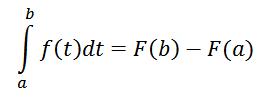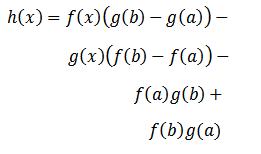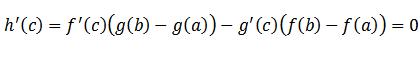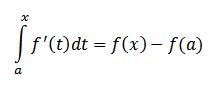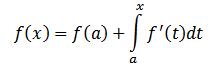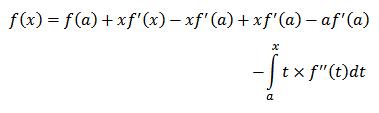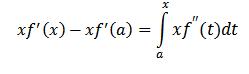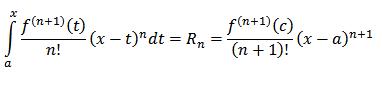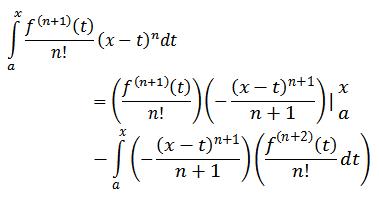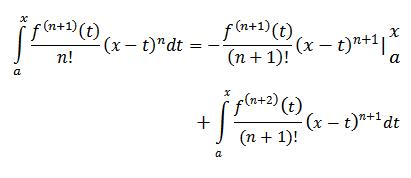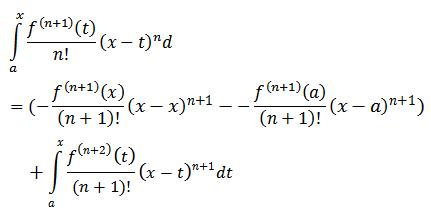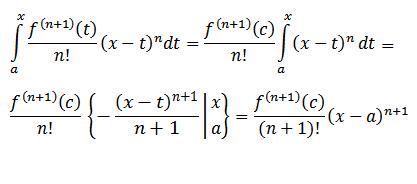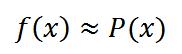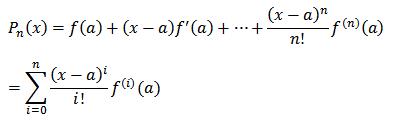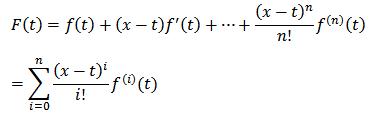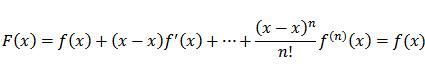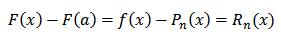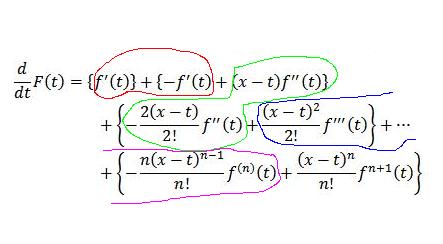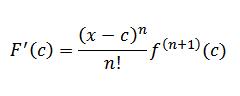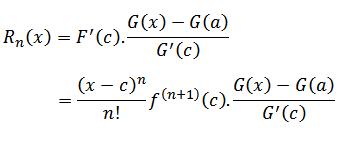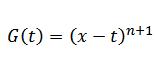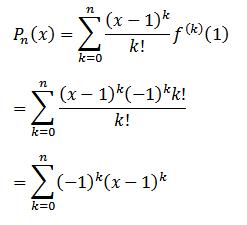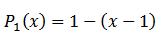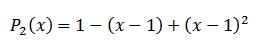محاسبات عددی

مجدداً سلام ،دیگه این تابستون و گرما و بی کاریش داره فشار میاره ناجور

واسه همین این بخش رو هم اضافه کردم ،چون خودم ناجور با آنالیز عددی حال می کنم تصمیم گرفتم بیام این موضوع رو هم اینرنتی کنم و آبروش رو ببرم :) ، منتها از این به بعد این جا بیشتر کد می زنیم ، کم تر اثبات می کنیم (هر چند خودم از اثباتاش بیشتر خوشم میاد) خلاصه میخواییم تو این قسمت دور همی بلایی سره آنالیز عددی بیاریم که کلاً پشیمون شه از به وجود اومدنش :) ، منتظر باشید !!!!

--------------------------------------------------------------------------------------------------------------------------

مقدمات:

هر کاری نیاز به یه سری مقدمات داره ، آدم غیبت هم که می خواد بکنه قبلش یه کم تخمه ای چیزی میاره که مجلس خوش بگذره:)

آنالیز عددی هم مثل بقیه کارا ، اونم نیاز به یه سری مقدمات داره ( حتی اون سری مقدمات هم نیاز به یه سری مقدامات دارن :) ) پس بهتره که قبلش اون مقدمات رو آماده کنیم.

جدای از هم این چرندیات که بالا نوشتم ، وجداناً آنالیز عددی درسیه که نیاز به پیش نیاز خاصی نداره و همین جوریش هم بسیار قابل درکه ،حالا کار نداریم تو دانشگاه ها ممکنه این درس رو بعد از یه درس دیگه ارائه بدن و بگن که این درس صد در صد نیاز به پیش نیاز داره ،ولی اینجا که دانشگاه نیست :) ،قوانینشون مال خوشون ، ما قانون خودمونو داریم :))

هدف آنالیز عددی در کل یه چیزه : آنالیز و تحلیل به روش عددی :)

یه زمانایی که هنوز کامپیوتر ماپیوتر ابداع نشده بود آدمهایی مثل نیوتن ( و از اون هم قدیمی تر آدمایی مثل Heron  ) دنبال روش های الگوریتمی یا تکراری بودن که بتونن با استفاده از اون روش ها به جواب های خاصی از بعضی مسائل با دقت خاص دست پیدا کنن،در ادامه سعی می کنیم با بعضی از این مسائل آشنا بشیم ،ولی در کل موضوع خیلی وسیع و گسترده ای و تو این چند خط نمیشه کمال مطلب رو فهمید :)

و اما پیش نیاز ها

حد تابع:

تعریف حد در ظاهر یکی از ساده تری تعاریف ریاضی (برای اونایی که الکی ادعا دارن) و در عمل یکی از پیچیده ترین مفاهیم ریاضی است .(اگه تو این جمله شک دارین برید ببیند نیوتن تونست به زبان ریاضی حد رو تعریف کنه یا نه؟؟ :) )

در اینجا ما فعلاً حد تابعی رو تعریف می کنیم که قبلاً هم دیدینش به احتمال زیاد:

می گیم حد   تابع f در نزدیکی نقطه a برابر با L می باشد به طوری که هر وقت که به a نزدیک میشیم (ولی دقیقاً بهش نمی رسیم) اونوقت f به L نزدیک میشه.

به قولی :

یعنی اگه یه بازه بین L-e و L+e انتخاب کنیم اونوقت بتونیم یه بازه بین a-d و a+d انتخاب کنیم به طوری که به ازای همه x هایی که توی این بازه دومیه هستن f(x) a توی اون بازه اولیه نزدیک L باشه :O

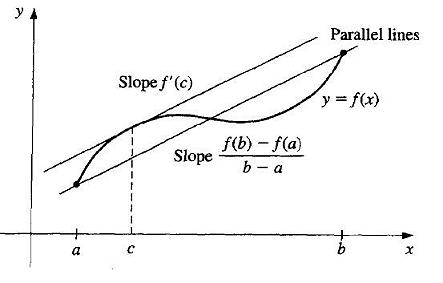
یعنی توی شکل زیر هر چه قدر که دو تا خط افقی رو به هم نزدیک کنیم بتونیم دو تا خط عمودی متاظر با اونا رو پیدا کنیم  که شرط بالا توش صدق کنه(شکل از هم چیز بهتر توضیح میده)

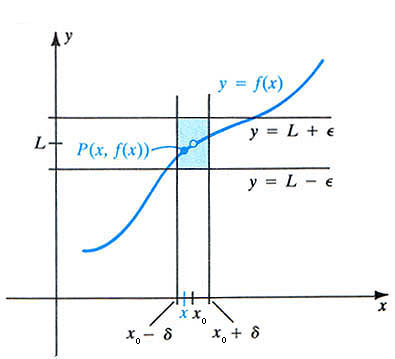
(راستی این شکل دزدیه :این نکته رو در جهت حفظ امانت گفتم :) )

تعریف پیوستگی :

می گوییم تابع f در نقطه a پیوسته است اگر حد آن در این نقطه موجود و با مقدار تابع در این نقطه (a)  برابر باشد.

مشتق:

هر گاه تابع f در نقطه a تعریف شده باشد و حد زیر موجود باشد:

در این صورت می گوییم f در نقطه a مشتق پذیر است و حد فوق را مقدار مشتق f در نقطه a می نامیم و آن را با f'(a)a نشان می دهیم.

اینم تعبیر هندسی مشتق (مجدداً عکس دزدیه :)) )

قضیه:اگر تابع f در نقطه a مشتق پذیر باشد آنگاه f در a پیوسته است.

قرار داد:

اگر X زیر مجموعه از R باشد آنگاه مجموعه تمام توابعی که بر X دارای n مشتق پیوسته هستند را با Cⁿ(X)a نشان می دهیم .همچنین تمام توابعی که از هر مرتبه مشتق پذیر هستند را با  C^∞(X)a نشان می دهیم ( e^x نمونه ای از این نوع توابع است).همین نماد گذاری را برای بازه [a,b] به صورت Cⁿ[a,b]a به کار می بریم ، هنگامی که n=1 باشد از نوشتن آن صرف نظر می کنیم.

قضیه مقدار اکسترمم:

اگر تابع f عضو C[a,b]a باشد آنگاه نقاطی مانند c و d موجودند به طوری که :

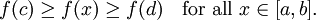
اینم تصویر مربوطه به این قضیه :(این که این تصویر مال کجاست تابلوئه :) )

باور کنید این قضیه خیلی مهمه!!!!!!!!!

قضیه رُل (Rolle's Theorem):

اگر تابع f بر [a,b] پیوسته و بر (a,b)  مشتق پذیر باشد و f(a)=f(b)a باشد آنگاه نقطه ای مانند c که a<c<b وجود دارد به طوری که f'(c)=0 است.

اثبات:

چون f بر [a,b] پیوسته است پس بنا در این بازه هم مقدار ماکسیمم داره و هم مقدار مینیمم!

حالا این مقادیر اکسترمم یا در نقاط انتهایی بازه اتفاق می افتن ، یا یه جایی داخل بازه

اگه داخل بازه اتفاق بیفتن دو حالت داره : یا در این نقطه مشتق صفره یا تعریف نشده است ، ولی ما گفتیم که fدر (a,b) مشتق پذیره ، پس نمی تونه مشتق در نقاط اکسترمم تعریف نشده باشه.

اگه ماکسیمم یا مینیمم یه جایی داخل بازه روی نقطه c اتفاق بیفته a<c<b اونوقت f'(c)=0 و کار تمومه!اگه این حالت اتفاق نیفته اونوقت هم ماکسیمم و هم مینیمم باید روی نقاط انتهایی بازه اتفاق بفتن.

می دونیم که هر مقدار تابع f روی بازه [a,b] بین مقادیر ماکسیمم و مینیممش قرار می گیره.

حال چون در این حالت فرض کردیم مینیمم و کاسیمم روی نقاط انتهایی بازه اتفاق میفتن و چون f در این نقاط برابره (بنا به فرضf(a)=f(b)b) پس تمام مقادیر تابع روی این بازه بین f(a)a      و f(b)b قرار میگیرن (ساندویچ می شن:) ) و نتیجه می گیریم که تو کل این بازه :

f(x)=f(a)=f(b)b

و این یعنی این که f یک خط افقیه که مشتق همه جاش صفره ، پس هر جای این بازه که عشقمون کشید می تونیم یه c انتخاب کنیم که توش f'(c)=0 باشه و تمام.

حالا بریم سراغ یه قضیه با حال تر و مهم تر:

قضیه مقدار میانگین (Mean Value Theorem):

اگر تابع f(x)a بر بازه [a,b] پیوسته و بر (a,b) مشتق پذیر باشد آنگاه نقطه ای مانند cبه طوری که a<c<b وجود دارد به طوری که:

اینم دو تا شکل که این قضیه رو توضیح می دن:

خب فکر کنم که شکل همه چیز رو خوب نشون میده ، اگه تو شکل های بالا نقطه a رو ثابت نگه دارم و تابع رو طوری بچرخونیم که f(b)b مقابل f(a)a قرار بگیره (یعنی بعد از چرخش داشته باشیم f(a)=f(b)b ) اونوقت این میشه همون قضیه رل ،ولی خب چون این استدلال خیلی خودمونیه بزارید یه استدلال درست درمون بیارم که قانع شید:

اثبات:

فرض کنید داشته باشیم:

 با استفاده از مقدار m یک تابع جدید معرفی می کنیم به نام g و به صورت زیر:

g(x)=f(x) - m*(x - a) - f(a)a

dچون g'(x)=f '(x) - m (از تعریف g مشتق بگیرید) پس g(x)b هم مثل f(x)b تو کل بازه مشتق پذیره.

داریم g(a)=f(a) - m*(a-a)-f(a) =0 و

g(b)=f(b) - m*(b-a) - f(a)a

با جایگذاری تعریف m به جای m داریم:

پس g(a)=g(b)=0 ،پس بنا به قضیه رُل نقطه c ای بین a و b وجود داره که g'(c)=0 ،ولی چون g'(c)=f'(c) - m نتیجه می گیریم که g'(c)=0=f'(c) - m =0 و این یعنی f'(c)=m

 و اگه تعریف m رو به جای m بزاریم اثبات قضیه به پایان میرسه(دیگه این کار رو خودتون انجام بدین)    :).

و اما شاخ قضیه های این بخش :

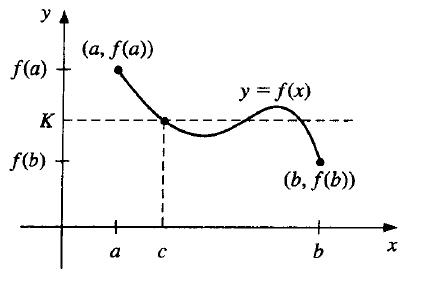
قضیه مقدار میانی (Intermediate Value Theorem):

اگر تابع f(x)x بر بازه [a,b] پیوسته باشد و K مقداری بین f(a)a و f(b)b باشد آنگاه نقطه ای مانند c در [a,b] وجود دارد به طوری که f(c)=K.

خب فعلاً پیش نیاز ها تا همینجا بسه ، یه سری پیش نیاز دیگه هم نیاز داریم که به موقعش اونا رو هم می گم.

نمه نمه دیگه بریم سر اصل مطلب!!!!

حل معادله f(x)=0 یا همون پیدا کردن ریشه معادله f(x)x:

فرض کنید که یه تابع f داریم و می خواهیم یه ریشه اون رو پیدا کنیم؟؟؟ چه راهی پیشنهاد می کنید؟؟؟اگه تابع یه چند جمله ای درجه یک یا دو باشه ،زارت از همون فرمول معروفه استفاده می کنیم و جواب رو به دست میاریم ، ولی اگه درجه چند جمله ای زیاد باشه یا اصلاً تابع مورد نظر چند جمله ای نباشه چه گلی به سرمون بزنیم؟؟؟:)

در ادامه سعی می کنیم یه روش هایی رو بررسی کنیم که یه ریشه معادله رو پیدا می کنن.

فعلاً توجهمون رو به توابعی که روی یک بازه خاص پیوسته هستند معطوف می کنیم.

حالت خاصی از قضیه رل:

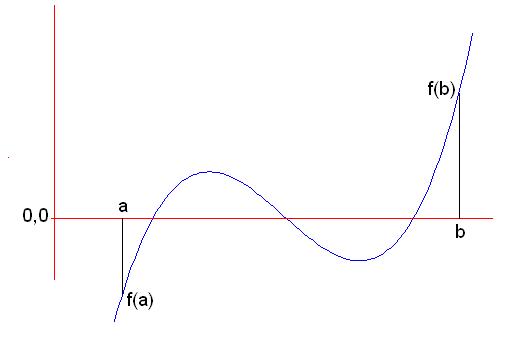
فرض کنید که f روی بازه [a,b] پیوسته باشه و تابع روی این بازه یه سرش زیر محور x=0 باشه و سر دیگه اش بالای محور x=0 یعنی داشته باشیم f(a)*f(b)<0 ،اونوقت ادعا می کنیم که تابع توی این بازه یه صفر داره .( وقتی می گیم تابع یه صفر داره یعنی یه نقطه ای وجود داره که تو اون f(x)=0  است.

مثل شکل زیر:

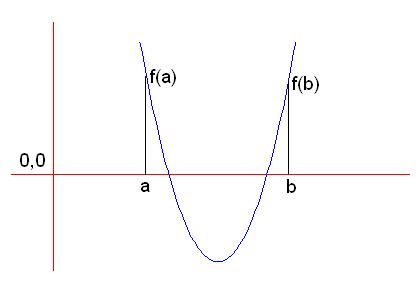
توجه کنید که عکس قضیه بالا درست نیست ، یعنی اگه f(a)*f(b)>=0 باشه نمی شه گفت که f توی این بازه ریشه نداره ، مثل شکل زیر:

خب ، حالا که چی؟؟؟گیریم که یه بازه داشته باشیم که توش f(a)*f(b)<0 باشه ، چه دخلی به حال ریشه f توی این بازه داره؟؟؟

ببینیم چی کار می شه کرد؟؟

اگر c نقطه وسط a و b  باشه (یعنی c=(a+b)/2 ) اونوفت f(c)c سه حالت داره:

1) یا f(c)=0 است که در این حالت c ریشه f  است (این "است" خیلی ضایعست:) ، ولی جایگزین خوب براش ندارم:) ) .

2) f(c)>0  است ، در این حالت یا f(c)c با f(b)b هم علامته یا با f(a)a ، اگه f(c)c با 

f(b)b هم علامت باشه اونوقت با f(a)a مختلف العلامته ، پس یه ریشه توی بازه [a,c] داریم ، اگه f(c)c با f(a)a هم علامت باشه اونوقت با f(b)b مختلف العلامته پس یه ریشه تو بازه [b,c] داریم ، در هر صورت پس از محاسبه c می تونیم توی یه بازه که نصف بازه اولیه است به دنبال ریشه باشیم.

3) اگر f(c)<0 باشه هم استدلالی مشابه با استدلال بالا میاریم.

نتیجه کلی رو میشه به صورت یک الگوریتم تکراری در آورد که به الگوریتم تنصیف مشهوره:

الگوریتم تنصیف(Bisection Algorithm):

تابع پیوسته f و بازه [a,b] داده شده است به طوری که f(a)*f(b)<0 (توجه کنید که این شرط ضروریه شروع الگوریتمه ).

1) نقطه c=(a+b)/2  را محاسبه می کنیم.

2) اگر sign(f(c))=sign(f(a))a آنگاه قرار می دهیم a=c و b=b (یعنی b بدون تغییر می مونه)

و به 4 می رویم.

3) اگر sign(f(c))=sign(f(b))b آنگاه قرار می دهیم a=a و b=c .

4) اگر بازه مورد نظر به اندازه کافی کوچک باشد آنگاه می توانیم c را به عنوان تقریبی از ریشه f بیان می کنیم.در غیر این صورت به 1 می رویم.

نکته:برای خروج از الگوریتم بالا می تونیم چند تا شرط بزاریم و با یکی از اونا از برنامه خارج بشیم:

1) f(c)c به اندازه کافی به صفر نزدیک بشه ( اندازه کافی که دیگه به نظر خودتون بستگی داره)

2) بازه مورد نظر به اندازه کافی کوچیک شده باشه.

3) الگوریتم به تعداد مورد نظر (مثلا M تا ، که M هم به خودتون بستگی داره) تکرار شده.

نکته:به جای اینکه از شرط f(a)*f(b)<0 استفاده کنیم ، علامت های f(a)a و f(b)b رو با هم مقایسه می کنیم ، چون وقتی بازه کوچیک میشه استفاده از ضرب میزان خطاش زیاده !!!!!!

و اما کد نویسی:

اول کد sign که بچه بازیه:) :

و اینم کد الگوریتم تنصیف :

تو کد بالا مقادیر M و delta و eps رو هر جور که خودتون دوست دارید مقدار دهی کنید .

تابع f تو کد بالا یه تابع است که مقدار تابع ریاضی ای که قصد داریم ریشه اش رو محاسبه کنیم ،توی یه نقطه خاص محاسبه می کنه.

نکته : استفاده از c=(a+b)/2 ممکنه به دلیل خطاهای کامپیوتری باعث بشه که c خارج بازه بیفته به جاش بهتره که c رو به صورت c=a+e محاسبه کنید!!!!

e همیشه اندازه نصف بازه رو نگه می داره.

نکته دیگه ای هم اگه مونده خودتون بگید( تو رو خدا تعارف نکنید :) )

------------------------------------------------------------------------------------------

جلسه دوم:

تا اینجا یه مقداری پیش نیاز های ریاضی رو بررسی کردیم و با یکی از کاربرد های محاسبات عددی آشنا شدیم ، الآن شما یک روش در دست دارید که می تونید با اون یه ریشه رو توی یه بازه به دست بیارید ولی اگه یادتون باشه گفتیم که انتخاب بازه اولیه مهمه ،همچنین گفتیم که تعیین شرط خروج به میل خودتون بستگی داره.

حالا فرض کنید که سه نفر داریم به نام های

جمشید 

خشایار

چنگیز

یه معادله f بهشون می دیم و می گیم که با استفاده از روش تنصیف ریشه f رو محاسبه کنند ، تضمین هم می کنیم که f تنها یه ریشه ساده داره.

این سه نفر به این صورت عمل می کنند:

جمشید بازه اولیه [2,20000] رو انتخاب می کنه و الگوریتم رو 20 بار اجرا می کنه

خشایار بازه اولیه [1,5] رو انتخاب می کنه و الگوریتم رو 3 بار اجرا می کنه

چنگیز بازه اولیه  [1,3]  رو انتخاب می کنه و الگوریتم رو 50 بار اجرا می کنه

فرض کنید که هر سه نفر بازه اولیه رو درست انتخاب کردند یعنی برای هر سه نفر بازه های انتخاب شده دارای شرط f(a)*f(b)<0 است.

سوالی که پیش میاد اینه:

1) جواب کدوم یکی از این سه نفر دقیق تره؟؟؟

2) دقیق ترین جواب چه قدر دقیقه؟؟؟اصلاً رضایت بخش هست؟؟ (ممکنه هر سه نفر گند زده باشن و جواباشون به درد نخوره)

اول بیایید بازه های انتخابی این سه نفر رو مورد بررسی قرار بدیم ببینیم کدومشون بازه بهتری رو انتخاب کرده:

به طور شهودی میشه گفت که انتخاب چنگیز انتخاب بهتریه چون طول بازه کوچیکتره ، ولی چرا ما بازه های با طول کمتر رو ترجیح می دیم؟؟

فرض کنید که بازه [a,b]  به ما داده شده و ما می دونیم که r ریشه معادله f عضوی از این بازه است ، ما می خواهیم نقطه ای به نام x عضوی از این بازه رو انتخاب کنیم و اون رو به عنوان تقریبی از r بیان کنیم .

چون هم r و هم x عضوی از بازه [a,b] هستند فاصلشون از هم دیگه نمی تونه بیشتر از فاصله ی b از a باشه درنتیجه اگه اختلاف r و x رو با |x-r| نشون بدیم (قدر مطلق تفاضل این دو مقدار) اونوقت:

به عبارت |x-r|  می گیم خطای مطلق.

این مقدار حداکثر اختلاف بین تقریب x و مقدار r رو نشون میده. در نتیجه قبل از شروع الگوریتم انتخاب چنگیز منجر به خطای کمتری میشه.

حالا ببینیم وقتی این سه نفر الگوریتم رو اجرا می کنن چه اتفاقی می افته:

قبل از شروع الگوریتم بازه ای که داریم بازه [a,b]  است ، خطای مطلق این بازه هم که بالا اشاره کردیم به صورت b-a  هست ، در اولین اجرای برنامه نقطه c وسط این بازه انتخاب میشه ، پس از این انتخاب ریشه یا تو سمت چپ c قرار داره یا سمت راستش و یا خودش ریشه است در هر صورت بازه جدیدی داریم که ریشه توشه و طول این بازه نصف طول بازه اولیه است( یا بازه سمت چپیه یا بازه سمت راستیه) پس بعد از اولین اجرای برنامه خطا به صورت زیر می باشد:

از اون جایی که پس از تعیین بازه جدید الگوریتم این بازه رو جایگیزین بازه قبلی می کنه ، پس فعلاً بازه جدیده طولش نصفه بازه اولیه است ، در دومین اجرای الگوریتم این بازه جدیده هم نصف میشه پس خطا به صورت زیر میشه:

 و پس از n بار اجرای الگوریتم خطا به صورت زیر خواهد :

خطای الگوریتم تنصیف پس از n تکرار:

می بینیم که خطا به صورت نمایی کاهش پیدا می کنه (همچنین می بینیم که جوابی که چنگیز حساب می کنه از بقیه دقیق تره ).

جواب قسمت دوم سوالی که در ابتدا مطرح شده بود رو خودتون حساب کنید (b=3,a=1,n=50).

خب تا اینجا با مفهوم خطای مطلق آشنا شدیم ، خطای الگوریتم تنصیف رو هم حساب کردیم ، ممکنه الآن پیش خودتون فکر کنید که الگوریتم تنصیف خیلی الگوریتم خفنیه ولی سخت در اشتباهید در ادامه پته این روش رو میریزیم رو آب :) .

همچنین ممکنه فکر کنید که خطای مطلق همیشه معیار خوبیه برای خطا ولی نشون می دیم که اینطور نیست.

مثال

هنگامی که از قلی می پرسیم فاصله تو از جایی که نشسته ای تا در یخچال که در آشپزخانه قرار داد چه قدر است پاسخ می دهد 9 متر ، محاسبات نشان می دهد فاصله دقیق او تا در یخچال 8 متر است در نتیجه قلی به میزان 1 متر در محاسبات خود اشتباه کرده است . هنگامی که از قلی می پرسیم فاصله تو از جایی که نشسته ای تا در اتاق مدیر دانشکده چه قدر است پاسخ می دهد 30329 متر.محاسبات نشان می دهد که فاصله دقیق او تا در اتاق مدیر دانشکده 30328 متر است لذا قلی به میزان یک متر در محاسبات خود اشتباه کرده است . 

مشاهده می کنیم که در هر دو حالت قلی به میزان 1 متر دچار خطا شده است در کدام یک از این دو حالت خطا به نظر شما قابل چشم پوشی است ؟؟؟

مطمئناً در حالت دوم (اینکه قلی چگونه می تواند فاصله خود تا دانشکده را اینگونه محاسبه کند همچنان بی پاسخ مانده است :) )

در اینجا به طور ذهنی برای قابل قبول بودن یا قابل قبول نبودن تقریب میزان خطای مطلق را با اندازه واقعی در مقام قیاس قرار می دهیم و سپس نظر می دهیم برای همین فکر می کنیم که خطای حالت دوم قابل چشم پوشی است  ، 

خطایی که در این حالت استفاده می کنیم به خطای نسبی معروف است و  به صورت زیر تعریف می شود.

اگر x تقریبی از r باشد خطای نسبی به صورت زیر خواهد بود:

توجه کنید که معمولاً به دلیل اینکه r از قبل مشخص نیست (و معمولاً بعداً هم مشخص نخواهد شد) لذا کمتر اتفاق می افتد که قادر به محاسبه دقیق خطای نسبی یا خطای مطلق باشیم ، در اکثر موارد سعی ما بر این است که برای این خطا ها یک حد بالا تعیین کنیم (مانند آن حدی که برای خطای الگوریتم تنصیف ارائه کردیم).

نکته: این که از خطای مطلق یا خطای نسبی استفاده کنیم به شرایط مسئله ای که قصد حل کردن آن را داریم بستگی دارد ، معمولاً هنگامی که r بزرگ باشد استفاده از خطای نسبی معیار مناسب تری است ، همچنین هنگامی که r نزدیک صفر باشد خطای مطلق معیار مناسب تری است.

فعلاً اجازه دهید تا کمی از مباحث نظری مربوط به خطا ها دور شویم و مجدداً به بررسی کاربرد ها بپردازیم.

تا الآن توانستیم یک حد بالا برای خطای الگوریتم تنصیف به دست بیاوریم ، سوال مهمی که الآن مطرح می شود این است : " آیا می توانیم قبل از شروع الگوریتم  تنصیف تعداد تکرار های لازم این الگوریتم برای اینکه خطا کمتر از مقدار معین eps باشد را تعیین کنیم؟؟؟" 

با اجازه بزرگ تر ها پاسخ این سوال مثبت است.:) :)

تا الآن تونستیم یه حد بالا برای خطای الگوریتم تنصیف تو تکرار n ام به دست بیاریم ، حالا می خواهیم ببینیم برای اینکه خطای این روش کمتر از eps بشه به چند تا تکرار نیاز داریم.

با توجه به حرف های بالا بعد از تکرار n ام باید داشته باشیم:

چون می خواهیم n رو به دست بیاریم باید اونو یه طرف به صورت جدا داشته باشیم،برای اینکار  2ⁿ رو می بریم اون ور ، b-a رو میاریم این ور:)

اینو میتونیم اینجوری هم بنویسیم:

حالا از طرفین لگاریتم می گیریم:

دیگه خواص لگاریتم رو جا نمیشه بخوام توضیح بدم (خودتون می دونید دیگه).

مثال:

برای یافتن ریشه معادله x²-2x-5=0  در بازه [3,4] با دقت 0.00001  به چند تکرار از الگوریتم تنصیف نیاز داریم:

در نتیجه برای این مسئله برای اینکه به دقت مورد نظر برسیم حداقل 17 تکرار لازمه.

نکته:مبنای لگاریتم رو هر چی که دوست دارید می تونید انتخاب کنید ولی بهتره اونو طوری انتخاب کنید که محاسبات ساده تر بشه معمولاً هم مبنای 10 انتخاب خوبیه ، من اینجا لگاریتم چند تا عدد رو تو مبنای 10 براتون آوردم که معمولاً به درد می خورن:

log(1) = 0.00
log(2) = 0.30
log(3) = 0.48
log(5) = 0.70
log(7) = 0.85
log(11) = 1.04
log(13) = 1.11
log(17) = 1.23
log(23) = 1.36

من اینجا تا دو رقم اعشار چاپ کردم ،ولی معمولاً تا یه رقم اعشار کافیه!!!!!(البته باید گرد کنید).

با اینکه خیلی دلم می خواد بیشتر رو این الگوریتم تنصیف بحث کنیم ،ولی باشه شاید در آینده ای نه چندان نزدیک دوباره روش بحث کردیم.

ولی فعلاً بیایید پرونده اش رو ببندیم:

نقاط قوت الگوریتم تنصیف:

1) شرطی که روی تابع f میزاره بسیار کمه (فقط کافیه که f توی بازه مورد نظر پیوسته باشه).

2)حد خطاش به سادگی قابل محاسبه است.

3)همواره همگراست (این مهم ترین خاصیتشه).

نقاط ضعف:

1) پیدا کردن بازه اولیه که شرط f(a)*f(b)<0 توش بر قرار باشه ممکنه سخت باشه.

2)همگراییش نسبت به خیلی از روش های دیگه کند تره(توضیح: اینکه می گم همگراییش کند تره یعنی اگه این و یه روش دیگه بخوان به یه دقت خاص برسن این روش نیاز به تعداد تکرار های بیشتری داره).

3) به راحتی نمیشه اون رو برای حل معادله هایی با ابعاد بیشتر بسط داد. (یعنی وقتی تعداد متغیر های تابع مورد نظر افزایش پیدا کنه دیگه به همین راحتی ها نمی تونیم از این روش استفاده کنیم.)

یه سری ضعف های دیگه هم داره این روش که فعلاً جاش نیست بگم.

و اما در مورد ضعف شماره یک:

چون متاسفانه عده قلیلی وجود دارن که بعد از دو سه خط کد زدن زارت ادعای برنامه نویسیشون میشه ممکنه که این عده قلیل فکر کنن که مشکل اول مشکلی نیست .

البته ممکنه یه عده غیر از دسته بالا (یعنی یه عده از غیر مدعیان) هم همچین فکری بکنند ، برای همین با مثال این موضوع رو مو شکافی می کنیم که خیال همه راحت شه:

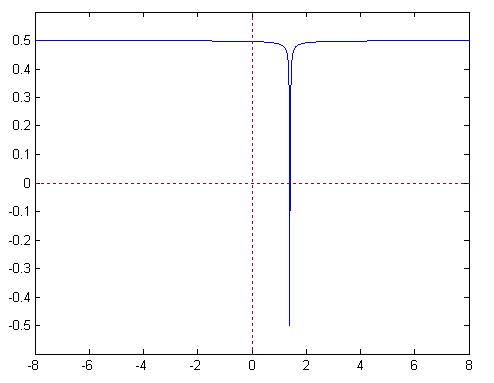
فرض کنید که تابع کلی f به صورت زیر باشه:

(کی میگه این تابع پیوسته نیست؟؟؟؟؟)

این تابع رو برای M=2,M=20 و M=200 براتون رسم کردم:

M=2

خب مثل اینکه برای M=2 پیدا کردن یه بازه که توش f(a)*f(b)<0 باشه خیلی سخت نیست. 

حالا بریم سراغ M=20:

M=20

فکر کنم تو این حالت یه کم برای کامپیوتر یا هر ماشین محاسباتی دیگه یه مقدار پیدا کردن بازه مناسب برای شروع الگوریتم تنصیف سخت باشه.

و اما این هم M=200:

M=200

می بینیم که با افزایش M پیدا کردن بازه مناسب برای شروع الگوریتم تنصیف هم سخت تر میشه .

نکته:

خواهشاً نیایید بازه مناسب رو دستی پیدا نکنید بعد بیایید بگید " بابا این که کاری نداره ، بیا اینم بازه مناسب" :) ، اگه اینجوری باشه که خوب اصلاً ریشه رو هم دستی محاسبه می کنیم! ، پس توجه کنید که ما دنبال روش های الگوریتمی هستیم که بشه اونا رو توی یه ماشین محاسباتی (معمولاً کامپیوتر) پیاده سازی کرد و خود این ماشین بتونه مسئله رو حل کنه. برای همین وقتی میگیم پیدا کردن بازه مناسب تو مثال بالا سخته منظور اینه که نوشتن یه برنامه کامپیوتری که از ماهیت f از قبل خبر نداره و بخواد بازه مناسب رو برای الگوریتم تنصیف پیدا کنه خیلی کار ساده ای نیست. حالا از ما گفتن بود.:) :)

در ضمن مثال بالا فقط یه مثال بود!!!!!!!

نکته پایانی این قسمت:معمولاً از این الگوریتم به عنوان یک مرحله ابتدایی برای الگوریتم های دیگه استفاده می شه به این صورت که اول با این روش یه ریشه تقریبی به دست میاریم و بعد با یه روش سریعتر دقت ریشه رو بهبود می بخشیم.

---------------------------------------------------------------------------------------------

جلسه سوم:

قبل از ادامه بحث ریشه یابی بهتره که یه کم با "تقریب" آشنا بشیم ، "تقریب" خیلی کلمه کلی ایه و جا واسه بحث زیاد داره که امیدوارم در آینده بتونیم خوب روش بحث کنیم. ولی الآن فقط می خوام یه کوچولو با این موضوع آشنا بشیم که بعدش یه قضیه رو مطرح کنم چون از این به بعد از این قضیه ه که می خوام بگم خیلی استفاده می کنیم. (خیلی که چه عرض کنم شاید خیلی خیلی و ...)

اصلاً تقریب یعنی چی؟؟

یه موقع هست که ازتون می پرسن فلان درس رو چه قدر خوندی ( یا چه قدر بلدی ؟؟ معمولاً این دو تا واژه اشتباهاً به جای هم به کار میرن:)) و جواب شما اینه که 80 در صد مطالب کتاب رو بلدم.

یه موقع هم می گید که 80 درصد فصل یک رو بلدم.

در هر دو حالت شما با یک تقریب خوب (80 در صد) به یک مفهومی احاطه دارید ولی جواب اول موقع امتحان های پایان ترم به درد می خوره (زمانی که کل کتاب تو امتحان میاد) و جواب دوم موقع امتحان های کلاسی (موقعی که فصل به فصل امتحان گرفته میشه).

یه همچین چیزی رو میشه در مورد توابع ریاضی هم به کار برد (مخصوصاً توابع پیوسته چون اگه یادتون باشه ما فعلاً داریم با توابعی کار می کنیم که تو بازه خاص [a,b] پیوسته هستند).یعنی گاهی اوقات دوست داریم یک تقریب از یک تابع توی یه بازه کلی داشته باشیم و گاهی اوقات یک تقریب از یک تابع توی یک نقطه.

ولی تو توابع تقریب به چه دردمون می خوره؟؟؟ خب خیلی وقت ها پیش میاد که تابع اصلی ای که می خواهیم باهاش کار کنیم تابع پیچیده ایه یا کار کردن باهاش در حالت کلی سخته در این صورت دوست داریم که به جای تابع اصلی از یک تابع ثانویه استفاده کنیم که رفتار تابع اول رو تقلید کنه (یعنی تقریبی از اون باشه ) و کار کردن با هاش هم ساده تر باشه.

مثلاً فرض کنید یه تابع f داشته باشید که مثلثاتی باشه ، یه نفر میاد میگه فلانی چرا از این تابع استفاده می کنی ؟؟مگه دیوانه ای؟؟ بیا از تابع g استفاده کن که چند جمله ایه دقیقاً هم کار f رو انجام میده! خوبیه توابع چند جمله ای اینه که کار کردن باهاشون خیلی خیلی ساده است ، هم خیلی ساده میشه مقدار یک چند جمله ای رو توی یه نقطه محاسبه کرد و هم اینکه راحت میشه ازش مشتق گرفت و خیلی کار های دیگه.

در این قسمت هم قصد داریم که با تقریب یک تابع به وسیله چند جمله ای ها در نزدیکی یک نقطه خاص آشنا بشیم ، یعنی می خواهیم چند جمله ای هایی رو پیدا کنیم که در نزدیکی یه نقطه خاص مثل تابع اصلی رفتار کنن. وقتی می گیم نزدیکی یه نقطه خاص یعنی یه بازه خیلی کوچیک که اون نقطه خاص رو در بر گرفته باشه. این نوع تقریب رو بهش می گیم تقریب نقطه. 

بیایید با یه مثال بیشتر با این قضیه آشنا بشیم و الکی خودمون رو گیج نکنیم.

فرض کنید تابع اصلی f به صورت f(x)=cos(x)x  باشه.ما می خواهیم توی یه بازه خیلی کوچیک نزدیکای pi/4 با این تابع کار کنیم ، هر چند f(pi/4)=cos(pi/4)x محاسبه اش ساده است ولی برای بقیه مقادیر نزدیک pi/4 محاسبه این تابع خیلی ساده نیست (حد اقل من که حوصله ندارم یه چیزی مثل cos(0.2+pi/4)x رو محاسبه کنم:) ).

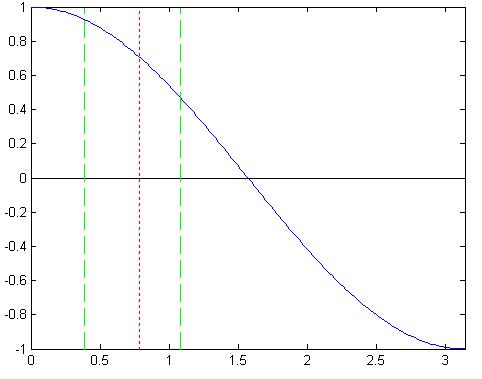
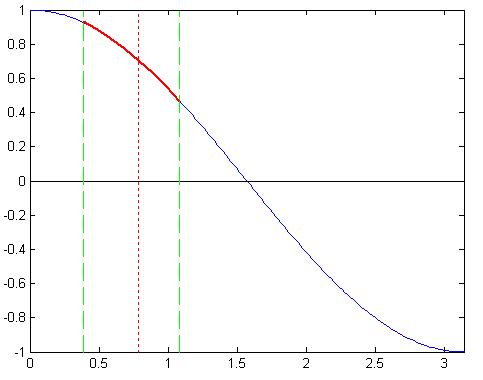
خب اول ببینیم نمودار f=cos(x)x چه جوریه؟؟ مخصوصاً نزدیکای pi/4 .

روی نقطه pi/4 یه خط عمود رسم کردم که راحت تر اونو پیدا کنید ، حالا می خواهیم یه بازه کوچیک انتخاب کنیم نزدیکای pi/4  ، مثلاً انتخاب زیر:

[pi/4 - 0.4 , pi/4 + 0.3]

اینم شکل این بازه:

حالا می خواهیم یه تابع ساده تر انتخاب کنیم و توی این بازه به جای cos(x)x از اون استفاده کنیم.

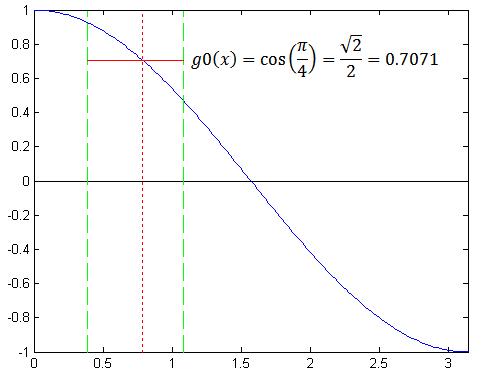
ساده ترین انتخاب اینه که خط y=cos(pi/4)x رو به عنوان تقریب در نظر بگیرم ،خیلی هم کار کردن باهاش ساده است:) ، بالاخره هر چی باشه یه تقریب از تابع است دیگه، نیست؟؟؟ اتفاقاً خیلی وقت ها انتخاب های اینجوری جواب هم میدن حالا شاید تو این مثال خیلی جالب نباشه:)

پس اولین تابعی که به عنوان تقریب انتخاب می کنیم میشه این:

ببنیم این تابع توی بازه مورد نظر چی جوری تابع اصلی رو تقریب می کنه:

انصافاً تقریب ضایع ایه:دی ، چرا؟؟؟ چون هر چی از pi/4 که دور تر میشیم اختلاف بین این تابع و تابع اصلی به شدت بیشتر میشه.

نکته: این تقریبی که استفاده کردیم در حقیقت یه چند جمله ای درجه صفر بود.

نکته:این تقریبی که استفاده کریم فقط یک ویژگی تابع اصلی رو تقلید می کرد و اونم اینکه توی نقطه pi/4 مقدارشون یکی بود ، یعنی تنها ویژگی مشترک این تابع با تابع اصلی به صورت زیر بود:

حالا فرض کنید که یه دوست ریاضی دانی داشته این طرفا قدم میزده که یه هو اتفاقی اومده این تقریبی که ما استفاده کردیم رو دیده ،اول کلی بهمون می خنده و بعد هم میگه که " مرد حسابی (یا زن حسابی) تو که داری این تابع رو با یه خط تقریب می کنی ، حداقل یه خطی می کشیدی که شیبش توی نقطه pi/4 با شیب تابع اصلی تو نقطه pi/4 یکی باشه :) :)" ،بعد این حرف هم این دوست ریاضی دانمون هر هر کنان میره :)

انصافاً حرف بدی هم نمیزنه این دوست ریاضی دانمون اگه یه خط می کشیدیم که شیبش با شیب تابع اصلی یکی بود اون وقت ، وقتی از pi/4 دور میشیم خطا با سرعت کمتری افزایش پیدا می کرد.

اما!

اما !!!

اما ببینیم پشت این حرف این (یارو) ریاضی دانه چی نهفته است؟؟؟

وقتی می گیم شیب خط توی نقطه خاص یعنی داریم در مورد مشتق تابع توی اون نقطه حرف می زنیم (تعریف مشتق که یادتونه ، عکسش اون بالا مالا هست برید یه نگاه بندازید یادتون بیاد).

پس باید یه تابع g1 انتخاب کنیم که تو شرط های زیر صدق کنه:

قبلاً فقط یه شرط داشتیم تونستیم یه چند جمله ای درجه صفر به دست بیاریم الآن که دو تا شرط داریم می تونیم یه چند جمله ای درجه یک به دست بیاریم چون یک چند جمله ای درجه یک به فرم زیره :

در نتیجه دو تا ضریب مجهول (a و b) داریم ، که با داشتن دو تا شرط میشه این ضرایب رو به دست آورد.

با توجه به تعاریف داریم:

چون می خواهیم که شیب g1 و f توی نقطه pi/4 با هم برابر باشن پس باید داشته باشیم:

و به همین سادگی یه دونه از ضرایب مجهول g1 به دست اومد.

از طرفی چون می خواهیم g1 تابع f رو توی نقطه pi/4 تقریب کنه مقدار این دو تا تابع هم باید توی نقطه pi/4 با هم برابر باشه لذا:

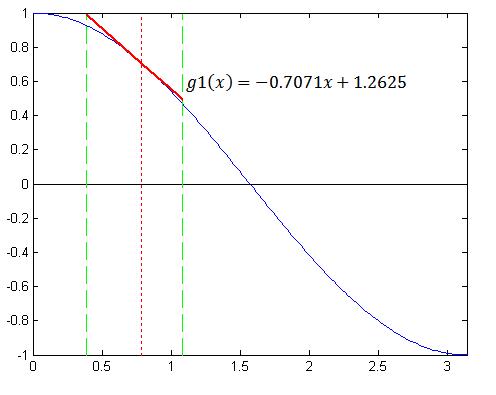
تا اینجا ضرایب مجهول a و b رو به دست آوردیم ، حالا با جایگذاری این مقادیر تو تعریف تابع g1  داریم:

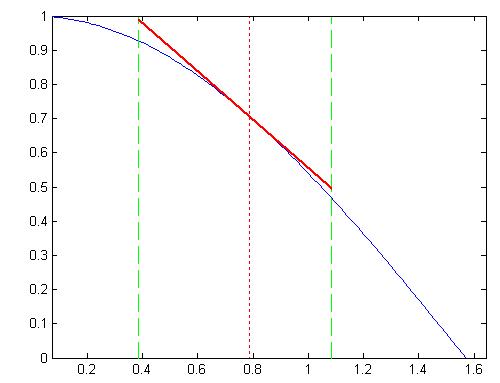
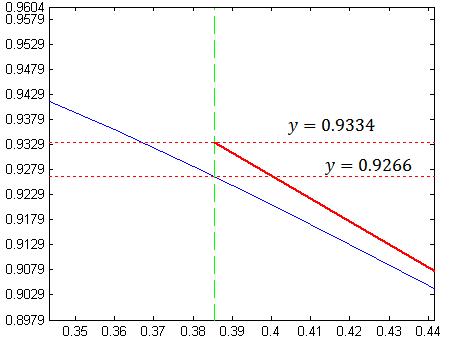
حالا ببینیم این تقریبی که به دست آوردیم چی جوریه؟؟به شکل زیر توجه کنید:

انصافاً از تقریب قبلی که خیلی بهتره، نه؟؟؟بزارید یه زوم شده اش رو هم ببینیم:

شما رو نمی دونم ، ولی من خودم که از روشی که استفاده کردیم خیلی خوشم اومد طلبه شدم این کارایی رو که انجام دادیم به صورت یک فرمول کلی در بیارم که بشه باهاش هر تابع پیوسته و یک بار مشتق پذیر (حداقل یک بار) f رو توی یه نقطه خاص تقریب کرد.یعنی باید مسئله زیر رو حل کنیم:

فرض کنید g1 یک چند جمله ای درجه 1 باشد که تابع پیوسته و یک بار مشتق پذیر (حداقل یک بار) f را در نقطه  x₀ تقریب می کند ، فرمولی کلی برای g1 برحسب f بیابید.

چون g1 یک چند جمله ای درجه 1 می باشد پس رابطه کلی آن به صورت زیر است:

چون شیب g1 باید با شیب f در نقطه x₀ برابر باشد لذا داریم:

یعنی به همین راحتی یه رابطه برای a به دست آوردیم.

از طرفی مقدار f و g1 نیز باید در نقطه x₀ برابر باشند ، مقدار a رو هم که به دست آوردیم  پس:

حالا b رو هم به دست آوردیم ، با قرار دادن a و b در تعریف g1 داریم:

تازه داشتیم با این روشی که به دست آوردیم حال می کردیم که دوباره سر و کله این یارو ریاضی دانه پیدا میشه و میگه:

"داری با چند جمله ای ها تابع f رو تقریب می کنی؟؟"

ما: آره ، چطور مگه؟؟

ریاضی دان:" خب چرا از خط صاف برای تقریب استفاده می کنی؟"

ما:چشه مگه؟؟

ریاضی دان:" با اینکه تونستی شیب f رو تقلید کنی ولی انحناش رو نتونستی!"

ما:آها، یعنی یه چند جمله ای استفاده کنم که بشه باهاش یه خم ایجاد کرد؟؟

ریاضی دان: "آره ، با هر چند جمله ای از درجه بیشتر از یک می تونی یه منحنی ایجاد کنی"

ریاضی دان که داشت همچنان دور می شد گفت " فقط یه چیزی یادت نره ، سعی کن چند جمله ای ای انتخاب کنی که جهت انحنا یا تقعرش در جهت انحنای f باشه"!

اول ببینیم این جمله آخرش یعنی چی؟

اگه ریاضیات دبیرستان یادتون باشه تقعر و انحنای یه چند جمله ای رو میشه با استفاده از مشتق دوم تعیین کرد ، اگر مشتق دوم مثبت باشه تقعر رو به بالا و اگه منفی باشه تقعر رو به پایین داریم.

برای مثال به شکل زیر نگاه کنید:

هر سه تا منحنی t1 و t2 و t3 سعی دارن که تابع f رو توی نقطه a تقریب کنن.

هر سه تا منحنی هم شیبشون توی نقطه a  با شیب f برابره (مشتق اولشون یکیه).

ولی t2 یه خط صاف یا چند جمله ای درجه یکه و مشتق دومش صفره و اطلاعات خاصی در اختیار ما قرار نمی ده.

t1 جهت تقعر و انحناش هم جهت با f هست برای همین نقاط انتهایی t1 خیلی از f دور نشدن ولی تقعر و انحنای t3 در خلاف جهت f هست و نقاط انتهایی t3 به شدت از f دور میشن. چون جهت تقعر t1 و f برابره می تونیم بگیم که مشتق دومشون باهم هم علامته (هر دو مثبتن).

نکته: مشتقات متوالی هر تابع هر کدوم یک خصوصیت از تابع رو بیان می کنن ، برای همین یه چند جمله ای ، ای که بتونه مشتقات بیشتری از یک تابع رو تقلید کنه بیشتر شبیه اون میشه.برای مثال اگه مشتق اول و دوم چند جمله ای p1 با مشتق اول و دوم f برابر باشه و مشتق اول و دوم و سوم چند جمله ای p2 با مشتقات اول و دوم و سوم f برابر باشه ، اونوقت p2 بهتر از p1 رفتار f رو توی یه نقطه خاص تقلید می کنه.البته این ویژگی فقط توی خود نقطه مورد نظر صادقه و در مجاورت اون ممکنه درست نباشه ، یعنی ممکنه یه چند جمله ای مشتقات بیشتری از یک تابع رو توی نقطه a تقلید کنه ولی وقتی از a دور میشیم خطاش بیشتر بشه(نسبت به یه چند جمله ای که مشتقات کمتری رو تقلید می کنه) ، مثالی از این موضوع رو بعداً می بینیم.فعلاً زیاد روش فکر نکنین.البته این بحث ها بیشتر مربوط میشه به آنالیز حقیقی و نظریه توابع تحلیلی که شاید بعداً به صورت جداگانه روشون کار کردیم.

خب بریم رو ادامه بحثمون.

این دفعه می خواهیم یه چند جمله ای پیدا کنیم که هم مقدارش توی نقطه x₀ با  f برابر باشه و هم مشتق اول یا شیبش و هم مشتق دومش(در حقیقت ما می خواستیم که مشتق دومش هم علامت باشه ولی چون داریم روی یه نقطه کار می کنیم ترجیح دادیم که از شرط تساوی استفاده می کنیم).

چون سه تا شرط داریم می تونیم از یک چند جمله ای درجه دو برای اینکار استفاده کنیم چون یک چند جمله درجه 2 به صورت زیره و سه تا مجهول a و b و c داره:

روند کار که دیگه اومده دستمون اول ضریب a رو به دست میاریم:

اول می خواهیم که مشتق دوم g با مشتق دوم f توی نقطه pi/4 برابر باشه، پس:

خب این از a.

از طرفی مثل قبل شیب f و g هم باید توی نقطه pi/4 با هم برابر باشه:

دیگه اینکه f و g باید مقدارشون هم توی نقطه pi/4 برابر باشه که اصلاً گفتن نداره!ولی می گیم:)

خوب الآن هم a و هم b و هم c رو داریم یعنی:

اگه نتیجه رو رسم کنیم ،وحشتناکه (این کاربرد وحشتناک از اون کاربرد معکوس هاست،یعنی تقریب خیلی خوبه):

انصافاً عجب تقریبی شده، بزارید یه تصویر زوم شده هم ببینیم (فقط ابتدای بازه زوم می کنیم)

می بینیم که با یه چند جمله ای درجه 2 تونستیم یه تقریب خیلی عالی نزدیک نقطه  x₀  به دست بیاریم ، البته ممکنه این روش همه جا به این خوبی جواب نداه ولی امکانش هم هست که خیلی جاهای دیگه همینجوری خوب عمل کنه ، پس با نگاه به نیمه پر لیوان بیایید این روشی رو که به کار بردیم براش یه فرمول کلی در بیاریم:

فرض کنید g2 یک چند جمله ای درجه 2 باشد که تابع پیوسته و دو بار مشتق پذیر (حداقل دو بار) f را در نقطه  x₀ تقریب می کند ، فرمولی کلی برای g2 برحسب f بیابید.

چون g2 یه چند جمله ای درجه قراره باشه شکل کلیش به صورت زیره:

چون می خواهیم مشتق دوم g2 و f تو نقطه x₀ با هم برابر باشن ،پس با همین مشتق دوم کار رو شروع می کنیم که ساده تره:

به همین راحتی a به دست میاد .

خب شیب f و g2 هم که دیگه باید حتماً برابر باشه ،اصلاً راه نداره!در نتیجه:

خب اینم از b ، فقط یه دونه دیگه مجهول مونده که باید حساب کنیم ، اونم c :

می دونیم که قراره توی نقطه x₀ مقدار f و g2  با هم برابر باشن:

حالا که a و b و c رو به دست آوردیم باید این ضرایب رو بزاریم تو تعریف g2 :

حالا از f و مشتقاتش توی نقطه x₀ جدا جدا فاکتور گیری می کنیم:

خب اینم از فرمول خوبه که دنبالش بودیم.

حالا یه تمرین واسه خودتون:

فرض کنید g3 یک چند جمله ای درجه 3 باشد که تابع پیوسته و سه بار مشتق پذیر (حداقل سه بار) f را در نقطه  x₀ تقریب می کند ، فرمولی کلی برای g3 برحسب f بیابید.

راهنمایی:فرض کنید در نقطه x₀ مشتق سوم f و g3 با هم برابرن.

اگه تنبلی نکنید و چند جمله ای های درجه چهار ،پنج و ... رو هم به دست بیارید جرقه های توی ذهنتون زده می شه که ممکنه بتونید یه فرمول کلی درست درمون حدس بزنید ، البته ممکنه تا همین الآنشم فرمول کلی رو حدس زده باشید

ادامه ایده بالا ما رو به سمت قضیه پایین رهنمون می کنه:

قضیه تیلور:

اگر f تابعی باشد که در نزدیکی نقطه x₀ بی نهایت بار مشتق پذیر باشد،آنگاه در نزدیکی x₀ می توان f را به وسیله مجموع چند جمله ای ها تقریب کرد و این تقریب به شکل زیر خواهد بود:

ولی معمولاً هم f بی نهایت بار مشتق پذیر نیست و هم اینکه ما وقت و حوصله بی نهایت بار مشتق گیری از f رو نداریم :) ، در نتیجه معمولاً فقط از چند جمله از بسط بالا برای تقریب استفاده می کنیم که در این صورت باید یه میزان خطایی رو با جان و دل بپذیریم.

مثلاً تو همین مثال قبلیه دیدیم که استفاده از تنها چند جمله اول این بسط چه قدر می تونه خوب باشه.

در نتیجه معمولاً قضیه بالا رو به صورت زیر بیان می کنیم که بهش قضیه تیلور با جمله باقی مانده هم می گن:

قضیه تیلور با باقی مانده:

اگر f بر بازه [a,b] بتواند n+1 بار مشتق پذیر باشد و x₀ نیز عضو [a,b]  باشد آنگاه به ازای هر x عضو [a,b] نقطه c ای وجود دارد به طوری که:

 

که P و R به صورت زیر هستند:

به رابطه P در بالا ، چند جمله ای تیلور درجه n ام f حول نقطه  x₀ گفته می شود.

در رابطه بالا c مقداری بین x و x₀ است که به انتخاب x وابسته است و معمولاً آن را با

c(x)x  نشان می دهند ولی در اینجا برای سادگی شکل فرمول تنها از نماد c استفاده کردیم ولی خواننده باید بداند که این مقدار به انتخاب x بستگی دارد.

به R در رابطه بالا جمله باقی مانده یا خطای تقریب یا خطای برشی گفته می شود.دقیق تر آن است که بگوییم R شکل لاگرانژ جلمه باقی مانده است چون رابطه R را می توان به شکل های دیگری نیز بیان کرد که شاید در آینده به آن شکل ها نیز اشاره شود.

(اه ، خسته شدم چه قدر کتابی حرف زدم :) )

خب قبل از اینکه این قضیه رو اثبات کنیم ، بریم یه چند تا پیش نیاز ببینیم:

یک یاد آوری از مشتق:

اگه از طرفین این رابطه انتگرال بگیریم خواهیم داشت:

یکی از انتگرال ها رو می بریم اون طرف تا به رابطه زیر برسیم که به انتگرال گیری جز به جز مشهوره:

معمولاً هم این رابطه به صورت زیر بیان می شود:

و یه یاد آوری خیلی خیلی مهم:) :)   :

خب بریم یه چند تا قضیه دیگه هم ببینیم و پرونده این درس رو ببندیم.(مثلاً قرار بود بیشتر کد بزنیم کمتر قضیه بیاریم ولی چه کنم که دست خودم نیست با قضایا بیشتر حال می کنم ، اگه بیخ و بن یه موضوعی رو خوب بفهمید زدن کد میشه ماست:) ).

و اما چند قضیه ی پایانی این درس:

قضیه مقدار میانگین وزن دار برای انتگرال ها (Weighted Mean Value Theorem for Integrals ):

اگر f و g بر بازه [a,b] پیوسته و انتگرال پذیر باشند و در این بازه g(x)>=0 باشد آنگاه عددی مانند c بین a و b وجود دارد به طوری که :

اثبات:

قضیه مقدار اکسترمم رو یادتون هست (گفته بودم باور کنید این قضیه خیلی مهمه!یادتونه؟) خب طبق اون قضیه چون f بر بازه بسته [a,b] پیوسته است پس توی این بازه کرانداره (محدوده) ،پس مقادیر x₀ و x₁ وجود دارند که تمام مقدایر f در بازه مذکور بین مقدار تابع f در این دو نقطه قرار می گیرند یعنی:

حالا چون g در کل بازه فوق بزرگتر مساوی صفر هست پس می تونیم اون رو بدون هیچ درد سری توی رابطه بالا ضرب کنیم (چون به هیچ وجه توی این بازه امکان نداره که g بتونه جهت نامساوی ها رو عوض کنه ، چون برای اینکار باید حداقل یه جا منفی باشه که خدا رو شکر هیچ جای بازه فوق g منفی نیست:) )

با خیال راحت می تونیم از نامساوی فوق توی بازه a تا b انتگرال بگیریم:

توجه کنید که f(x₀)x و f(x₁)x مقادیر عددی هستند (مقدارن دیگه!) پس می تونیم اونا رو از انتگرال بیاریم بیرون:

حالا اگه داشته باشیم:

که اون وقت چون g توی این بازه همواره بزرگتر مساوی صفره ،پس از رابطه فوق می فهمیم که g باید تو کل بازه متحد با صفر باشه! و اگه g همواره متحد با صفر باشه اونوقت رابطه ای که همون اول گفتیم بدیهی ، بدیهیه:)

منظورم رابطه زیره(فرض کنید g همیشه صفر باشه اونوقت دیگه جایی برای سوال باقی می مونه؟ )  :

، پس فرض می کنیم که g متحد با صفر نباشه و :

در این صورت می تونیم آخرین نامساوی ای رو که دیدیم بر انتگرال فوق تقسیم کنیم:

حالا یه بار دیگه یه کاربرد دیگه از قضیه مقدار میانی: قضیه مقدار میانی یادتونه چی می گفت؟ می گفت اگر f بر [a,b] پیوسته باشه و K مقداری بین f(x₀)x و f(x₁)x  باشه اونوقت نقطه ای مانند c بین x₀ و  x₁ وجود داره که توش f(c)=K.(البته توجه کنید که x₀ و x₁ خودشون هم عضو این بازه هستن پس هر نقطه ای که بینشون باشه باز تو همین بازه است:) )

خب حالا اگه تو رابطه بالا اون کسر خوبه رو به عنوان K در نظر بگیریم اثبات قضیه تموم میشه:

اگه تو قضیه بالا داشته باشیم g(x)=1، اونوقت به قضیه مهم و مشهور زیر می رسیم:

قضیه مقدار میانگین برای انتگرال ها (Mean Value Theorem for Integrals):

اگر f بر بازه بسته [a,b] پیوسته و انتگرال پذیر باشد آنگاه نقطه ای مانند c بین a و b وجود دارد به طوری که:

یا به عبارتی:

دیگه اثبات این قضیه هم با خودتون (وجداناً برای این یکی که اثبات نمی خواهید؟:) )

اینم یه عکس برای اینکه قضیه قبلی بهتر براتون جا بیفته :

قضیه اساسی حساب (Fundamental Theorem of Calculus) :

اگر f تابعی پیوسته و حقیقی مقدار بر روی بازه بسته [a,b] باشد و به ازای هر x عضو این بازه F تابعی به صورت زیر باشد:

اونوقت F بر [a,b] تابعی پیوسته و بر (a,b) مشتق پذیره و تابع اولیه f به حساب میاد یعنی به ازای همه x های عضو (a,b) خواهیم داشت:

همچنین (قسمت مهم و به درد بخورش):

اثبات قضیه رو هم فعلاً نمیارم چون حسش نیست :-) ،ولی خودتون برید دنبالش چون اثباتش هم نکات جالبی داره (البته شاید بعداً اثباتش رو اضافه کردم).

قضیه مقدار میانگین کوشی یا قضیه مقدار میانگین توسعه یافته

(Cauchy's Mean-Value Theorem,Extended Mean-Value Theorem):

قبل از اینکه این قضیه رو بگم یه نکته رو بگم فردا بین علمای بلاد اختلاف نیفته: بعضی جا ها این دو تا قضیه (مقدار میانگین کوشی و مقدار میانگین توسعه یافته) رو یکی می گیرن ،بعضی جا ها هم با یه مقدار اختلاف کوچیک در بیان صورت قضیه ،این دو تا قضیه رو متفاوت می گیرن ، اینجا من یه جوری صورت قضیه رو میارم (با یه کم برش مرش:) ) که نه سیخ بسوزه و نه کباب و در نتیجه بشه این دو تا قضیه رو یکی در نظر گرفت!

و اما قضیه:

اگر f و g بر [a,b]  توابعی حقیقی مقدار و پیوسته باشن و بر (a,b) مشتق پذیر باشن آنگاه نقطه ای مانند c بین a و b وجود دارد به طوری که:

اثبات:

تابع h(x)x رو به صورت زیر تعریف می کنیم:

می بینیم که طبق تعریف h این تابع هم مثل f و g بر [a,b] پوسته است و بر (a,b) مشتق پذیره.

همچنین h(a)=0 و h(b)=0  هستن.(خودتون این یه مورد رو چک کنید دیگه!)

چون h(a)=h(b)=0 هست پس طبق قضیه رُل نقطه ای مانند c بین a و b وجود داره که توش h'(c)=0 هست.یعنی:

و اثبات تمام می شود!(این مدل اثبات رو خوب درک کنید چون خیلی کار راه اندازه).

با کمی بی احتیاطی میشه رابطه قضیه قبل رو به صورت کسری در آورد (البته بی احتیاطی نیست ، بلکه باید یه سری شرایط جدید اعمال کنیم که این دیگه به عهده خودتون ،در حقیقت تفاوت قضیه کوشی و قضیه توسعه یافته هم در همین شرط هایی که است که برای صحت شکل کسری اعمال می کنن که امیدوارم خودتون این شرط ها رو در بیابید:) ).

و شکل کسری به صورت زیره:

نقطه ای مانند c بین a و b وجود دارد که:

این همه پیش مقدمه و قضیه گفتم که بالاخره بریم سر اصل مطلب یعنی همون "قضیه تیلور" که اگه خوب برامون جا بیفته و پرونده اش رو درست و حسابی ببندیم بعداً می بینید که خیلی استفاده ها میشه ازش کرد.

خب پس بر می گردیم به قضیه تیلور:

قضیه تیلور با باقی مانده:

اگر f بر بازه [a,b] بتواند n+1 بار مشتق پذیر باشد و x₀ نیز عضو [a,b]  باشد آنگاه به ازای هر x عضو [a,b] نقطه c ای وجود دارد به طوری که:

 

که P و R به صورت زیر هستند:

به رابطه P در بالا ، چند جمله ای تیلور درجه n ام f حول نقطه  x₀ گفته می شود.

برای این قضیه اثبات های مختلفی وجود داره و معمولاً هم بحث اثباتش جز مباحث آنالیز حقیقی هست ، اثباتاش هم قشنگن و هر کدوم نکاتی ظریف و مطالبی آموزنده دارن.

اینجا به دو شکل این قضیه رو اثبات می کنیم که اون قضیه هایی که قبلاً دیدیم به یه دردی بخورن حد اقل :دی

اثبات اول ، با استفاده از انتگرال ها:

قبلاً از طریق قضیه اساسی ریاضی یاد گرفتیم که :

اگه این عبارت رو یه کم این ور اون ور کنیم می تونیم اون رو به صورت زیر بنویسیم:

اینجا از اون جاهایی است که من همیشه می گم ما عادت کردیم به چیزای ریز نگاه نکنیم و دنبال چیزای بزرگ باشیم که بنده اعتفاد شدیدی دارم که  این تفکر غلط رو تو مدرسه و دانشگاه به ما یاد دادن :دی

اگه خوب به عبارت قبلی نگاه کنیم می تونیم اون رو به صورت زیر ببینیم:

انتگرال گیری جز به جز رو که دیگه همتون بلدید  ، پس عبارت بالا رو می شه به صورت زیر دید:

اینم محض یاد آوری برای اونایی گه انتگرال گیری جز به جز یادشون نیست:

پس عبارت قبلی رو با استفاده از انتگرال گیری جز به جز میشه به صورت زیر نوشت:

تو جمله بالا انتگراله خیلی به دل خوش نمیاد ، انگار یه چیزی کمه ، مخصوصاً اینکه یه جمله منفی پشتشه ، برای همین برای تمیز کاری و یه سری مقاصد دیگه جمله xf'(a)-xf'(a)z رو به عبارت بالا اضافه می کنیم که چون این مقدار در حقیقت صفر هست پس نباید به کسی بر بخوره:دی

حالا یه نموره دست بندی می کنیم این عبارت رو:

حالا یه چشم تیز بین می خوام تا بفهمه که :

توجه کنید که تو عبارت بالا x متغیر انتگرال نیست بلکه t متغیر انتگراله (معمولاً خیلی ها تو این یه تیکه یه ساعت گیر می کنن :دی ) در نتیجه اون x ه کاملاً بی آزار است.

حالا که اینو فهمیدیم، شکل انتگرالی این عبارت رو جایگزین می کنیم تو رابطه آخریه:

دو تا انتگرال ها رو که جون میده قاطی کنیم:

یه تمیز کاری دیگه هم انجام بدیم به صورت زیر میشه:

خب قضیه رو از کجا شروع کرده بودیم؟؟؟ از یه انتگرال که از a تا x گرفته می شد ، حالا دوباره یه انتگرال داریم که از a تا x گرفته می شه ، اگه دو باره همین روشی رو که به کار گرفتیم برای این انتگرال به کار ببریم و این روند رو همینجوری n بار ادامه بدیم اونوقت من بهتون قول می دم که پس از n بار تکرار میشه f رو توی نقطه x به صورت زیر نوشت:

در حقیقت اون انتگراله شکل دیگه ای از جمله باقی مانده تو بسط تیلوره ،یعنی باید نشون بدیم:

پس ادعامون شامل دو قسمت میشه ، قسمت اول رو با استفاده از استقرای ریاضی اثبات می کنیم ، پایه استقرا رو در حقیقت نشون دادیم فقط مونده حکم استقرا:

حکم استقرا :

اگر پس از n بار استفاده متوالی از انتگرال گیری جز به جز بتوان تقریب f(x)x را حول نقطه a به صورت زیر نوشت:

آنگاه در دفعه n+1 ام استفاده از این تکنیک f(x)x به صورت زیر خواهد بود :

پس فقط کافیه نشون بدیم که:

اینم که دیگه کاری نداره ، باز دست به دامان انتگرال گیری جز به جز میشیم:

در این صورت داریم:

(بازم یاد آوری کنم که حواستون باشه متغیر انتگرال گیری t هست نه x ).

خب با استفاده از انتگرال گیری جز به جز خواهیم داشت:

انتگرال بالایی رو اینطوری نوشتم که قشنگ بدونید سر u و v توی انتگلرال گیری جز به جز چی اومد.حالا این انتگرال رو یه کم تمیز ترش می کنیم:

باز هم میشه تمیز کاری انجام داد (به نظر من همیشه باید از کثیف کاری شروع کرد و به تمیز کاری رسید :دی )

اون مقدار a تا x رو هم بالاخره محاسبه کنیم بنده خدا الآن یه عمره منتظره محاسبه شه ما هی اون این ور اون ور می بریم (بازم حواستون باشه t متغیر انتگرال گیری هست):

در نتیجه :

تا حالا اینقدر با انتگرال گیری جز به جز حال کرده بودید؟؟؟؟ :دی

حالا فقط مونده نشون بدیم که:

این که دیگه کاری نداره از قضیه مقدار میانگین وزن دار برای انتگرال ها استفاده می کنیم (یادتونه که؟):

با استفاده از تقسیم بندی بالا در قضیه مقدار میانگین وزن دار برای انتگرال ها داریم:

و اثبات بدین سان تمام می شود.

اثبات دوم ، استفاده از قضیه مقدار میانگین کوشی یا مقدار میانگین توسعه یافته:

اثبات قبلی ویژگی های جالب زیادی داشت ، یکیش اینکه از همون شروع اثبات می تونتسیم بفهمیم که یه مفهوم مثله تقریب تیلور رو چی جوری میشه توی ذهن پر وروند ، دوم اینکه رابطه جالبی بین تقریب n ام و n+1 بسط تیلور به دست آوردیم که این خودش در جایگاه خودش خیلی با ارزشه ، سوم اینکه کلی با انتگرال گیری جز به جز حال کردیم این همه کار برد از یه چیز ساده مثل انتگرال گیری جز به جز نشون می ده که هیچ وقت نباید چیزای ساده و کوچیک رو دست کم گرفت.

از این حرفا بگذریم ،این بار می خوام یه اثبات دیگه رو بهتون نشون بدم.این اثبات یه مقدار از لحاظ دیدگاه و مفهوم با اثبات قبلی تفاوت ها بنیادی داره.برای ارائه این اثبات یه بار دیگه تقریب تیلور رو با جمله باقی مونده مطرح می کنیم:

اگر f بر بازه [a,b] بتواند n+1 بار مشتق پذیر باشد و x₀ نیز عضو [a,b]  باشد آنگاه به ازای هر x عضو [a,b] نقطه c ای وجود دارد به طوری که:

 

که P و R به صورت زیر هستند:

به رابطه P در بالا ، چند جمله ای تیلور درجه n ام f حول نقطه  x₀ گفته می شود.

(توجه کنید که مثل اثبات قبلی این دفعه هم به جای x₀ از نماد a  استفاده می کنیم ، این کار فقط برای راحتی خودمه :) ، دیگه باید حواستون باشه :) :).  )

خب اگه خوب به به صورت قضیه نگاه کنیم می بینیم که یه تیکه اش خیلی مهمه و اون اینه:

ببینید همیشه میشه یه P دلخواه رو انتخاب کرد و ادعا کرد که این P می تونه f رو تقریب کنه ، یعنی همیشه می تونیم بگیم که اگه P یک عبارت دلخواه باشه آنگاه:

هیچ کسی هم نمی تونه بگه که ادعای ما صد در صد غلطه ، آره ممکنه این تقریب گاهی خطاش خیلی زیاد باشه و گاهی هم خیلی کم ولی در هر صورت P یک تقریبی از f هست که خودمون انتخابش کردیم (این که خودمون انتخابش کردیم خیلیه :) ) ، در هر صورت می خوام بگم کسی نمی تونه این ادعای ما رو زیر سوال ببره تا زمانی که در مورد میزان خطا ادعایی نداشته باشیم.

بزارید بهتر  براتون توضیح بدم ، فرض کنید که شما یه تابع دلخواه f دارید من می گم خط y=2 این تابع رو "تقریب " می کنه ، هیچ حرفی هم از میزان دقت این تقریب نمی زنم فقط می گم این خط می تونه تابع شما رو تقریب کنه ، اونوقت شما می تونید بگید که من اشتباه می کنم؟؟؟ اصلاً یه مثال واضح تر یادتونه برای معرفی ایده پشت تقریب تیلور اولین بار از یه خط صاف برای تقریب استفاده کردیم؟؟؟ کارمون اشتباه بود؟؟؟ مسلماً نه ، اون چیزی که مشکل داشت میزان خطا بود.

پس می خوام بگم تا وقتی که در ادعامون در باره خطای تقریب حرفی نزنیم هیچ کس نمی تونه به ما خرده بگیره ، هر کی هر چی گفت " می گیم ، آقا تو چی کار داری من هر میزان خطایی برام قابل تحمله :) ، اصلاً می خوام از همین تقریب استفاده کنم تا چشات در آد:) ).

ولی وقتی بیاییم حرف از خطا بزنیم اونوقت کار سخت میشه یعنی وقتی بیاییم یه P رو به عنوان تقریب f معرفی کنیم و بگیم:

اونوقت دیگه نمی تونیم واسه ملت گردن کلفتی کنیم بگیم " همینه که هه ، دلم می خواد از P استفاده کنم" ،هر وقت P رو محاسبه می کنیم باید بتونیم R رو هم محاسبه کنیم چون تو عبارت بالا از تساوی استفاده کردیم ، کم نیست ، خیلی ادعای بزرگیه (یه چند لحظه در موردش فکر کنید :) ) ، یعنی وقتی حرف از تساوی می زنیم خیلی ادعامون بزرگ میشه و نمی تونیم به سادگی از هر تقریب دلخواهی استفاده کنیم.

حالا این حرفا یعنی چی؟؟؟

یعنی توی بسط تیلور اینکه می گیم P می تونه f  رو تقریب کنه کسی رو ناراحت نمی کنه ،بلکه اون جمله باقی مانده است که خیلی زور داره :) ، در نتیجه باید چی کار کنیم ؟؟؟ باید R رو طوری به دست بیاریم که همه قانع شن ، یعنی هر وقت می گیم:

کسی نتونه به ما خرده بگیره:) ، برای اینکار به صورت زیر عمل می کنیم:

فرض کنید که  P_n(x)x تقریبی از f(x)x باشد یعنی :

می خواهیم نشون بدیم که :

به طوری که R_n(x)x به صورت زیر است:

(یکی از ویژگی های با حال اثبات قبلیه این بود که علاوه بر R همزمان رابطه P رو هم به دست می آوردیم ، در صورتی که ما P رو جز ادعاهای خودمون داریم و تنها کافیه که R رو به دست بیاریم ، حواستون هست چی می گم؟؟؟ ).

برای اثبات این موضوع می خواهیم از ترفندی استفاده کنیم که شاید براتون تازگی داشته باشه ولی این ترفند تو آنالیز (عددی ، حقیقی و .. ) خوب جواب می ده.

توجه می کنیم که تعریف P به صورت زیر هست:

یعنی داریم حول a تقریب می زنیم.

حالا یه تابع باحال F(t)t به صورت زیر تعریف می کنیم:

می بینید که تعریف F خیلی شبیه P هست ولی با هم فرق دارن توی P  ای که تعریف کردیم a ثابته و x  متغیره اصلیمونه ، توی تعریف F اصلاً a ای وجود نداره ، در ضمن اینجا t متغیره و x یه ثابته ، این تفاوت خیلی مهمه ، انصافاً بشینید یه یه ربع ، بیست دقیقه رو تفاوت P و F فکر کنید ارزش داره :).

حالا ببینیم F چه خاصیتی داره:

و :

جالب شد ، نه؟؟؟ وجداناً یه بار به این دو تا رابطه ای که به دست آوردیم خوب توجه کنید، ببینید چی از توش می کشید بیرون؟؟

بله درست فهمیدید اختلاف این دو تا دقیقاً همون چیزیه که دنبالش بودیم یعنی همون خطای تقریب:

حالا فرض کنید که یه تابع دلخواه G(t)t  داشته باشیم که توی [a,x] پیوسته و مشتق پذیر باشه (پیدا کردن یه همچین تابعی اصلاً کاره سختی نیست ،فعلاً فقط فرض کنید که یه همچین تابعی داریم :) )

اونوقت اگه به معلموماتمون رجوع کنیم (به قسمت های قبلی رجوع کنید) ، می بینیم که بنا به قضیه مقدار میانگین کوشی (شکل کسریش) خواهیم داشت:

و این یعنی :

چون G رو دلخواه در نظر گرفتیم محاسبه G'(c)c و G(x)-G(a)x نباید کار دشواری باشه ( در حقیقت باید G رو طوری انتخاب کنیم که این کار راحت هم باشه :دی).پس فقط می مونه محاسبه F'(c)c

پس فعلاً به G  فکر نکنید و روی محسابه مشتق F تمرکز کنید(نیازی نیست که تذکر بدم نسبت به t) ، محاسبه مشتق این تابع خیلی راحت تر از چیزیه که بشه فکرش رو کرد:

خیلی مشتق با حالی داره ، نه؟؟؟

توجه کنید که برای گرفتن مشتق از هر جمله ضربی F  از قانون زیر استفاده کردیم:

حالا اینجاش باحاله که هر جمله ای به جز جمله آخر ، میشه منفیش رو توی آکولاد بعدی پیدا کرد ، مثل شکل زیر:

در نتیجه :

و همه اینا یعنی :

حالا فقط می مونه انتخاب G که اونم دستمون کلی بازه:).

اگه G رو به صورت زیر انتخاب کنیم:

اونوقت فرم باقی مانده ای به دست میاد که به باقی مانده کوشی مشهوره.

و اگه G رو به صورت زیر انتخاب کنیم:

اونوقت شکل باقی مانده ای به دست میاد که به باقی مانده لاگرانژ مشهوره.

اینم از دومین اثبات.

و اما سخنان پایانی اندر باب تقریب تیلور:

با اینکه تقریب تیلور یه تقریب خیلی خوب و کار راه اندازه ولی همون طور که خودتون هم متوجه شدید فقط از اطلاعات حول نقطه x₀ استفاده می کنه در نتیجه در عمل نمیشه با استفاده از تقریب تیلور شکل کلی یک تابع رو تقلید کرد ، البته الآن ما جمله خطا رو داریم ولی در کل جمله خطا فقط برای دل گرمیه:) ، در حقیقت ما باید از دقت تقریبی که استفاده می کنیم مطمئن باشیم (البته تا حدودی) ، در ضمن محاسبه جمله خطا هم همیشه ساده نیست :) ، در نتیجه معمولاً وقتی از تقریب تیلور استفاده می کنیم که بخواهیم رفتار یه تابع رو توی یه بازه خیلی کوچیک نزدیک یه نقطه خاص تقلید کنیم ،مثلاً می تونیم تقریب sin(x)x رو نزدیک نقطه صفر به دست بیاریم بعد به جای اینکه از sin  استفاده کنیم از این تقریب توی یه بازه خیلی کوچیک نزدیک صفر استفاده کنیم.

متاسفانه دیده شده که استاد دانشگاه اومده سر کلاس اول جلسه از روی تنبلی یه تابع رو با تقریب تیلورش جایگزین کرده بعد هم تا آخر کلاس تو هر نقطه ای که عشقش کشیده از این تقریب استفاده کرده بدون اینکه متوجه باشه چه میزان خطایی رو داره متحمل میشه (شاید هم دانشجو ها بی سواد تلقی کرده بود که این کار رو کرده ،در هر صورت ... ) خلاصه اینکه از این جور کارا کم ندیدیم:)  چه توسط جماعت دانشجو و چه توسط جماعت اساتید ، لذا از شما خواننده محترم خواهشمندیم وقتی از تقریب تیلور استفاده می کنید حواستون باشه که چه قدر دارید از x₀ دور میشید و این دور شدن چه میزان خطایی رو ممکنه براتون به ارمغان بیاره :) :).

بزارید یه مثال خوب بزنیم.(مثال مشهوریه تو این زمینه)

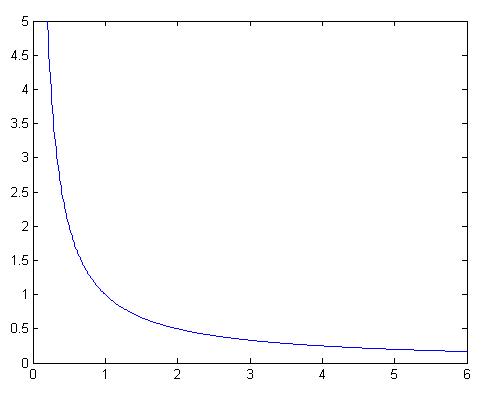
از تقریب تیلور برای تقریب تابع f(x)=1/x  حول نقطه 1 استفاده کرده و سپس مقدار f  را با استفاده از این تقریب در نقطه 4 محاسبه کنید.

یه عکس از f ببینیم تا یه جورایی قضیه کم کم دستمون بیاد :) .

البته فعلاً با دیدن f چیز زیادی دستگیرمون نمیشه.

خیلی راحت دیده میشه که مشتقات متوالی f توی نقطه 1  در رابطه زیر صدق می کنند:

در نتیجه تقریب تیلور درجه n ام f حول نقطه 1 به صورت زیر در میاد:

حالا چند تا تقریب تیلور از درجه مختلف رو آزمایش می کنیم تا ببینم توی نقطه 4 چه نتیجه دارن:

خب اول تقریب تیلور از درجه 1:

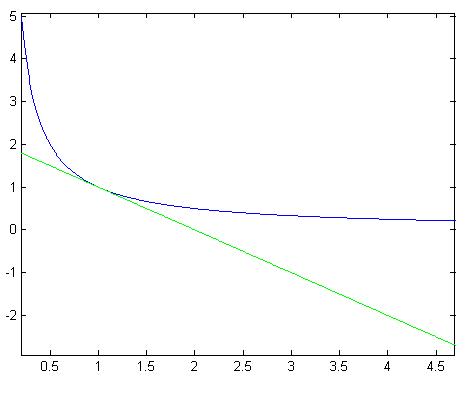
این تقریب به صورت زیره:

در حقیقت میشه گفت خطای تقریب افتضاحه :) ، چون P₁(4)=1-(4-1)=-2 هست ، در صورتی که مقدار واقعی f توی این نقطه 0.25 هست.

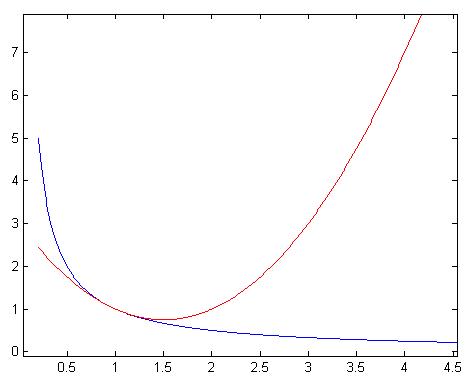
معمولاً انتظار میره که چند جمله هایی از درجات بالاتر در تقریب تیلور نتیجه بهتری داشته باشن ولی همیشه اینجوری نیست و این مثال یکی از مثال هایی است که نشون میده همیشه اینجوری نیست ، اجازه بدید تقریب تیلور از درجه 2 رو حساب کنیم:

اینم تصویر این تقریب:

این دفعه تقریب از قبل هم بدتر شده :) ، به طوری که P₂(4)=7 هست.

اگه همینجوری ادامه بدیم و از تقریب های با درجات بیشتر تیلور استفاده کنیم نه تنها تقریب بهتر نمیشه ، بد تر هم میشه ، شک دارید خودتون چند تا تقریب دیگه رو امتحان کنید.

در حقیقت این موضوع رو می تونید با تحلیل جمله خطا بررسی کنید که این کار رو به صورت تمرین به عهده خودتون می زارم.

پس نتیجه گرفتیم که:

1) وقتی حول نقطه a از تقریب تیلور استفاده می کنید و سپس برای محاسبه مقدار تابع در نقاط جدید از a دور میشید باید حواستون باشد ، کلاً تقریب تیلور توی یه بازه خیلی کوچیک نزدیک نقطه a خوب جواب میده و نمی تونه رفتار بازه رو به صورت کلی تقلید کنه

2) این تفکر که استفاده از تقریبات با درجات بالاتر تیلور منجر به تقریب بهتری میشه همیشه درست نیست و گاهی ممکنه تقریبات از درجات بالاتر خطای بیشتری هم داشته باشن ،پس هنگام تقریب این موضوع رو هم باید مد نظر قرار بدیم.

--------------------------------------------------------------------------------------------------------------------

به دلیل کش اومدن زیاد این صفحه ادامه مطالب رو می تونید تو قسمت دوم آموزش محاسبات عددی پیگیری کنید.