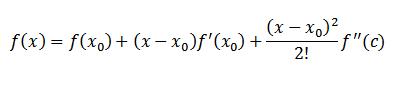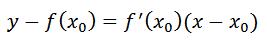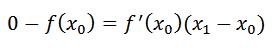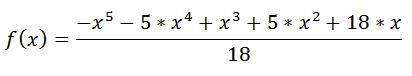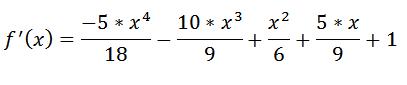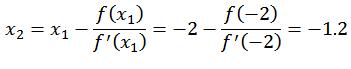محاسبات عددی- قسمت دوم
جلسه چهارم:
تا اینجا یه کم با مفهوم خطای مطلق و نسبی آشنا شدیم ، یه روش ساده و نه چندان سریع هم برای حل معادله f(x)=0 به دست آوردیم ، البته بهتره که بگیم یه روش برای به دست آوردن تقریب اولیه ، یه دو کم هم با بسط تیلور آشنا شدیم ،دیگه کم کم باید بریم سراغ روش های بهتر و اوضاع خودمون رو بهبود ببخشیم. این جلسه می خواهیم با یک روش بسیار مهم و البته قدرتمند و نسبتاً سریع برای پیدا کردن جواب های معادلات مختلف آشنا شیم و اون روش چیزی نیست جز روش نیوتن.
روش نیوتن(Newton's Method):
روش نیوتن در حقیقت یک روش عمومی و کلیه که در جاهای مختلفی و به شکل های متفاوتی میشه ازش استفاده کرد وقتی از این روش منحصراً برای پیدا کردن صفر های یک تابع حقیقی مقدار استفاده می کنیم به این روش نیوتن-رافسون (Newton-Raphson) هم می گن.
برای به دست آوردن روش نیوتن-رافسون چند راه مختلف وجود داره ، یکیش تعبیر هندسیه که من قبلاً ها خودم خیلی با تعابیر هندسی حال می کردم ، یه روش مبتنی بر بسط تیلوره چون اخیراً این بسط رو خوب درک می کنید (خوب درک می کنیم:دی) با این دیدگاه شروع می کنیم و این روش رو به دست میاریم ، اگه عمری باقی موند تعبیر هندسیش رو هم بیان می کنیم.(جدیداً با تعابیر مبتنی بر بسط تیلور خیلی حال می کنم:دی).
به دست آوردن روش نیوتن-رافسون با استفاده از بسط تیلور:
اگر f بر بازه [a,b] پیوسته و دو بار مشتق پذیر باشه و r ریشه تابع f(x)=0 باشد و x0 تقریبی از r باشد (یعنی r=x0+h باشه به طوری که h کوچیک باشه ) آنگاه چندجمله ای تیلور درجه 2 تابع f حول نقطه x0 را می توان به شکل زیر نوشت:
نکته: این مهمه که x0 تقریب خوبی از r باشه و همینجوری از روی هوا انتخاب نشده باشه ، مثلاً می تونید x0 رو با تکرار چند مرحله از الگوریتم تنصیف به دست بیارید.
به فرض که r رو داشته باشیم (البته r مجهوله و ما می خواهیم به دستش بیاریم ، حالا سر این قضیه الکی با من دعوا نکنید :دی ، گفتم به فرض که داشته باشیم:دی) با با جایگزاری r توی رابطه بالا داریم:
آخرین رابطه نشون میده که با استفاده از این تقریب خطا متناسب با h2 هست (بعداً در مورد نماد O بیشتر توضیح میدم ).چون فرض کردیم که x0 تقریب خوبی از r هست ، پس h باید کوچیک باشه در نتیجه h2 از اون هم کوچیک تره به طوری که می شه ازش چشم پوشی کرد ، در نتیجه می شه اینجوری نتیجه گرفت:
نتیجه می گیریم که که جمله زیر نسبت به x0 باید تقریب بهتری به r باشه:
خب حالا اگه روی این تقریب خوب تره یه اسم بزاریم که نمی میریم:دی، اسمش رو میزاریم x1:
خب حالا اگه همین بلایی رو که سر x0 در آوردیم ، سر x1 هم در بیاریم اونوقت می تونیم یه تقریب بهتر به نام x2 به دست بیاریم ، و در کل میشه این کار رو چند با انجام داد ، به این روش می گن یه روش تکراری ، یعنی یک بلایی رو چند بار سر نتیاج میانی بیاریم تا هی تقریب بهتر شه، نتیجه می گیریم که روش نیتون -رافسون رو میشه به صورت زیر نوشت:
توی رابطه بالا x0 رو باید از یه جای دیگه بیاریم:دی ، یعنی از قبل اونو داشته باشیم ، مثلاً استفاده از همون الگوریتم تنصیف برای به دست آوردن x0 روش خوبیه.
سوالی که الآن ممکنه پیش بیاد اینه که خب وقتی می خواهیم با الگوریتم تنصیف تقریب رو به دست بیارم چرا با همون ریشه رو حساب نمی کنیم؟ ، به جاش میاییم از اون به عنوان یه تقریب استفاده می کنیم و بعد با روش نیوتن-رافسون ریشه رو بهتر می کنیم؟ خب تا حدودی میشه گفت که جواب این سوال رو قبلاً دادم ، ولی فعلاً همینقدر بدونید که روش نیوتن-رافسون سریع تره ، اینکه از رو چه حسابی این حرف رو می زنم قضیه اش جداست که بعداً در موردش می بحثیم:دی.
و اینم کد ساده این روش در زبان جاوا :
تو کد بالا تابع f مقدار اون تابعی که دنباله ریشه اش هستیم رو در نقطه مورد نظر محاسبه می کنه ، تابع f_prim هم مشتقش رو توی اون نقطه محاسبه می کنه.
ولی معمولاً استفاده از یک سری تکرار های ثابت برای روش نیوتن-رافسون خیلی مناسب نیست چون ممکنه روش خیلی زودتر به جواب اصلی همگرا شه ، یا اینکه اختلاف دو تا تقریب متوالی خیلی زود کوچیک بشه ، برای همین بهتر برای توقف الگوریتم دو تا شرط دیگه هم اضافه کنیم ، یکی اینکه اگه جواب به اندازه کافی به صفر نزدیک شد یعنی قدر مطلق f توی نقطه مورد نظر به اندازه کافی کوچیک شد بیاییم بیرون ، یکی هم اینکه اگه دو تا نقطه متوالی تقریب، اختلافشون از یه میزان دلخواه دلتایی کوچیک تر شد الگوریتم رو متوقف کنیم ، کد زیر این دو تا شرط خروج رو هم داره:
یه نکته نه چندان مرتبط هم بگم برای جاوا کارا ، اگه توی کد توجه کرده باشید من ننوشتم Math.abs یا از این جور چیزا ، چون خوشم نمیاد :دی ، کثیف کاریه به نظر من که هی اسم Math رو بیاریم ، برای همین بنا به عادت معمولاً خط زیر رو اول برنامه هام میزارم و Math رو به صورت استاتیک ایمپورت می کنم ، اینجوری دیگه خیالم راحت میشه:دی
خب حالا که با روش نیوتن-رافسون آشنا شدیم ، الگوریتم تنصیف رو هم داریم ، بزارید یه مساله حل کنیم با جفت این روش ها ببینیم اصلاً این همه حرف می زنیم ، در عمل چه کاره ایم :) :).
مثال:
یک ریشه معادله f(x)=ex-x-2 را بیابید.
برای حل مسئله با روش تنصیف به یه بازه مناسب نیاز داریم ، برای حل مسئله با روش نیوتن-رافسون هم یه تقریب اولیه خوب می خواهیم ، اینکه یه برنامه کامپیوتری خوب چه جوری باید بتونه این مقدمات رو آماده کنه مسئله ای که باید از همین الآن ذهن شما خواننده خوب رو به خودش در گیر کنه (خدایی روش فکر کنید:دی) ، واقعاً کار ساده ای نیست. ولی چون فعلاً تازه کار هستید (تازه کار هستیم :دی) من هم بازه اولیه خوب به شما می دم برای الگوریتم تنصیف و هم تقریب اولیه نه چندان بد برای الگوریتم نیوتن-رافسون.منتها برای اینکه از این تقریف اولیه هایی که بهتون می دم خوشتون بیاد اونا رو به روش ترسیمی بهتون میدم.
نکته: تو بعضی کتاب ها از روش ترسیمی برای به دست آوردن تقریب اولیه نام می برن ولی وجداناً یه کم از دید برنامه نویسی بهش فکر کنید می بینید که ضایع است ، من اگه می تونم یه برنامه بنویسم که دو تا نمودار رو رسم کنه بعد بیام با چشم ببینم کجا این دو تا نمودار به هم می خورن ، چرا نباید بتونم یه برنامه بنویسم که خودش نقطه برخورد رو به دست بیاره و دیگه نیازی به چشم من نباشه ، این یه نکته ، نکته دوم اینکه اصلاً مگه به این سادگی هاست که من همیشه بیام یه تابع رو به صورت دو تا تابع بنویسم بعد هم زارت نقطه برخوردش رو به دست بیارم؟؟؟؟ اینه که روش ترسیمی آره یه زمانایی خوب بود اون موقع که ریاضی دان محترم خودش رو کاغذ می دونست داره چی رسم می کنه ولی اگه قراره باشه کار ها رو بسپاریم به یه ماشین فلزی ابله اون وقت روش ترسیمی به نظر من که جالب نیست :دی
(اه ، چه قدر فک می زنم؟؟؟؟ :دی)
و اما با همه این حرف ها روش ترسیمی:دی :دی:دی
معادله ex-x-2=0 رو میشه به صورت ex=x+2 هم نوشت ، در نتیجه محل تلاقی دو نمودار ex و x+2 همون صفر های f هستن.خب اینم نمودار این دو تا تابع و محل تلاقیشون:
می بینیم که دو تا نقطه تلاقی داریم ، ولی ما فقط یه ریشه می خواستیم پس از یکی از این نقطه تلاقی ها هم استفاده کنیم برامون کافیه ، برای همین بازه [1,2] رو برای شروع الگوریتم تنصیف و تقریب اولیه 1.5 رو هم برای شروع الگوریتم نیوتن-رافسون انتخاب می کنیم.
کد این دو تا الگوریتم رو هم که داریم ، هر کدوم رو تا 14 بار تکرار اجرا می کنیم (بقیه شرط های خروج رو هم غیر فعال می کنیم ):
کد f و f_prim رو هم خودتون به صورت زیر تغییر بدید:
اینم نتیجه 14 بار تکرار هر کدوم از این دو تا الگوریتم:
مقادیر x تا بیست رقم اعشار و قدر مطلق f تا 10 رقم اعشار نشون داده شدن:
Newton-Raphson :
x |f(x)|
--------------------------------------------------
1.21804229197217070000 0.1625208037
1.14977239230180750000 0.0077017702
1.14620258353996270000 0.0000200948
1.14619322068483730000 0.0000000001
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
1.14619322062058270000 0.0000000000
Bisection :
x |f(x)|
--------------------------------------------------
1.50000000000000000000 0.9816890703
1.25000000000000000000 0.2403429575
1.12500000000000000000 0.0447831511
1.18750000000000000000 0.0913737679
1.15625000000000000000 0.0217434275
1.14062500000000000000 0.0119017938
1.14843750000000000000 0.0048245865
1.14453125000000000000 0.0035625674
1.14648437500000000000 0.0006250069
1.14550781250000000000 0.0014702794
1.14599609375000000000 0.0004230112
1.14624023437500000000 0.0001009041
1.14611816406250000000 0.0001610770
1.14617919921875000000 0.0000300923
می بینیم که روش نیوتن-رافسون به لمحه ای (بعد از 5 تکرار) به جواب رسید در صورتی که روش تنصیف حتی بعد از 14 امین تکرار هم جواب چندان با حالی در نیاورد.
بعداً با مباحث همگرایی و سرعت همگرایی آشنا می شیم اونوقت خیلی علمی تر می تونیم بگیم که روش نیوتن-رافسون سریع تره یعنی چی.
اما هر سکه ای دو رو داره (البته اینجا ایرانه ممکنه سکه های چند رو یا یه رو هم دیده شه :دی ولی کلی داریم می صحبتیم :دی). پس قبل از اینکه الکی از روش نیوتن-رافسون برای خودمون بت بسازیم ، اجازه بدید پته اش را روی آب بریزیم.(البته حتی بعد از ذکر معایب این روش هم خواهیم دید که این روش قابل احترامه).
معایب روش نیوتن-رافسون:
قبل از ذکر معایب یه تعریف بیاریم ، بعد معایب رو بگیم.
تعریف:
اگر f(x)=(x - r)mg(x)x باشد و g(r)x مخالف با صفر باشد ، هرگاه m=1 باشد می گوییم r ریشه مرتبه 1 یا ریشه ساده f است و هر گاه m>1 باشد آنگاه می گوییم r ریشه تکراری از مرتبه m معادله f است.
و اما معایب روش نیوتن رافسون:
1) انتخاب نقطه اولیه در این روش مهم است و باید تقریبی خوبی از ریشه باشد ، معمولاً هنگامی که نقطه اولیه با ریشه فاصله زیادی دارد این روش همگرایی خوبی ندارد و یا ممکن است کلاً همگرا نشود .
2) اگر r ریشه ساده f باشد این روش به صورت درجه 2 همگرا می شود ولی هنگامی که r ریشه تکراری باشد درجه همگرایی کمتر از 2 خواهد بود.( درجه همگرایی رو هنوز نگفتم ولی این یه عیب رو آوردم که یه کم در مورد درجه همگرایی کنجکاو شید :دی ، فعلاً می تونیم اینجوری تعبیر کنیم که اگه r ریشه ساده باشه سرعت این روش خیلی خوبه ولی اگه ریشه تکراری باشه سرعتش خیلی خوب نیست).
3)این روش نیاز به محاسبه مشتق f دارد که گاهی ممکن است محاسبه مشتق f دشوار یا بسیار دشوار باشد :دی (گاهی چیه؟؟؟ اکثر موارد همینه:دی).
4) ممکن است در یکی از مراحل میانی مشتق f صفر شود یعنی f'(xn)=0 شود که در این صورت این روش منجر به واگرایی می شود .(بابا همگرا نمیشه دیگه؟ چیه؟یه عکس از این مورد رو خواهیم دید ، منتهی الآن زوده ، باشه بعداً :دی).
خب با اینکه این اشکالات رو میشه به این روش گرفت ولی اینطور هم نیست که هیچ راه فراری وجود نداشته باشه بعداً سعی می کنیم با این مشکلات دست و پنجه نرم کنیم و برشون پیروز شیم :) (چیه ؟ نکنه همین اول کاری کم آوردید؟؟نه بابا مرد (مراد از مرد اینجا جنس مذکر نیست کلاً مرد به معنای واقعی) باید سنگ زیرین آسیاب باشه :دی ).
قبل از اینکه جلوی این مشکلات در بیاییم باید اول خوب حریف رو بشناسیم:دی (توصیه رزمی)
برای همین قبل از همه کارا بریم یه بار دیگه روش نیوتن-رافسون رو بررسی کنیم منتهی این دفعه به صورت هندسی تعبیرش کنیم ببینیم چیزه جدیدی گیرمون میاد یا نه؟
تعبیر هندسی روش نیوتن-رافسون:
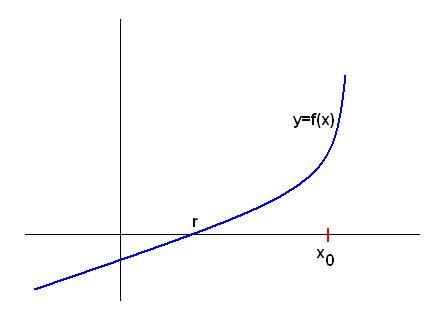
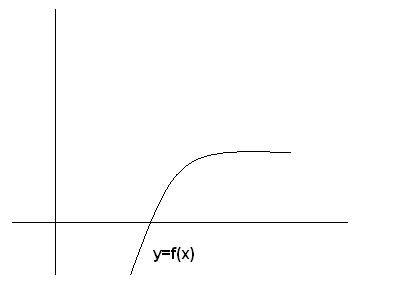
فرض کنید که نمودار تابع f برحسب x به صورت زیر باشه:
r ریشه تابع است ولی خب ما نداریمش :)) ، به جاش میاییم یه x0 رو که یه تقریبی به r هست رو به دست میاریم ، دیگه من کاری ندارم از کجا میارینش :) ، برید از یه جا گیرش بیارید ، این دیگه با خودتون ( می تونید از روش تنصیف استفاده کنید ، یا یه عالمه بازه پیدا کنید و عدد تصادفی تولید کنید یا ... خیلی کارا میشه کرد،بعداً بیشتر رو این موضوع می بحثیم).
خب حالا فرض کنید که x0 رو هم به صورت زیر انتخاب کردیم:
x0 تقریبی از r هستش ، فرض هم کنید که این تصویر زوم شده است و اختلاف r و x0 زیاد نیست (این فرض الآن مهم نیست ولی بعداً به دردتون می خوره)
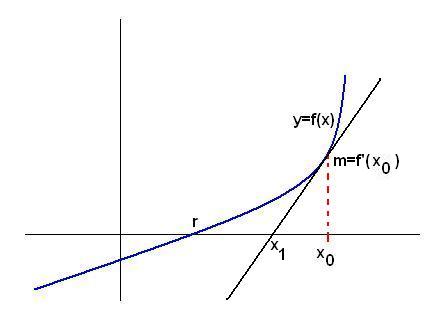
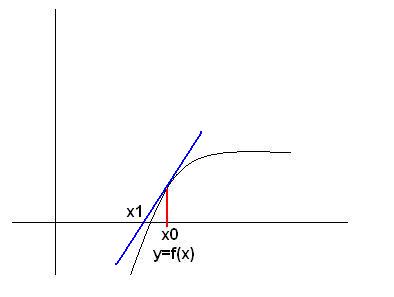
حالا می آییم خط مماس توی نقطه x0 بر روی تابع f رو رسم می کنیم:
محل برخورد این خط با محور x ها رو به عنوان تقریب جدیدی از r با نام x1 در نظر می گیریم ، اما چی جوری این نقطه رو محاسبه کنیم؟
خب اولین نکته این که شیب این خط رو داریم:) ، این خودش کلیه در حقیقت چون این خط ، خط مماس توی نقطه x0 است پس شیب خط میشه f'(x0)x .
می دونیم معادله خطی که با شیب معلوم m از نقطه x0,y0 عبور می کنه از معادله زیر به دست میاد (می دونیم دیگه نه؟؟:دی):
خب توی شکل بالا y0=f(x0)x هست و m=f ' (x0)x پس می تونیم بنویسیم:
حالا x1 نقطه ای هست که توی این خط صدق می کنه و به علاوه توش y=0 هست یعنی :
حالا فقط کافیه یه کم این رابطه رو تمیز کاری کنیم تا x1 به دست بیاد:
اینجوری x1 به دست میاد ، همین بلا رو سر x1 میاریم و x2 رو به دست میاریم و الی ....
خب اینجاست که ممکنه یه عده بچه زرنگ مچ منو بگیرن و بگن :" آهای فلانی این مثالی که زدی توش تابع f تقعرش رو به بالا بود و شیب خط توی نقطه x0 طوری میشد که نقطه بعدی یعنی x1 تقریب بهتری می شد ،اگه تقعر رو به پایین باشه چی؟"
پس اجازه بدید رو حرف این عده بچه زرنگ ها فکر کنیم:)
شکل زیر رو در نظر بگیرید:
بسته به این که تقریب اولیه یا همون x0 رو کجا انتخاب کنیم سه تا حالت مختلف ممکنه به وجود بیاد (تو هر سه مورد فرض کنید که x0 سمت راست r (ریشه f) هست، راستی چرا میگم سمت راست و نه سمت چپ؟ جلوتر جوابشو می بینیم ولی خودتون همین الآن روش فکر کنید)
یک: ممکنه x0 طوری انتخاب شه که در این حالت هم (با تقعر رو به پایین) x1 تقریب بهتری نسبت به اون باشه (این مورد رو بهش می گیم مورد خیر و برکت :دی)
شکل زیر رو در نظر بگیرید (جای x0 رو بهش دقت کنید):
توی این نقطه خط مماس رو رسم می کنیم و نقطه برخوردش با محور x ها رو به عنوان تقریب x1 در نظر می گیریم:
از رو شکل پیداست که x1 تقریب بهتریه نسبت به x0.
دو:ممکنه x0 طوری انتخاب شه که کلاً روش واگرا شه (این مورد دقیقاً آب پاکی رو دست آدم ریخته:دی ، دیگه هر وقت اوضاعتون اینجوری شد شما را توصیه می کنم به پیدا کردن یک نقطه اولیه دیگه:دی)
راستی فکر می کنید این اتفاق یا چیزی شبیه اون موقعی که تقعر رو به بالا باشه اتفاق می افته؟ اگه آره ، چه وقتایی؟؟
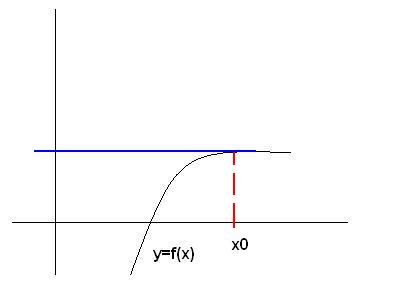
به شکل زیر دقت کنید:
اگه توی این نقطه خط مماس رو رسم کنیم موازی با محور x ها در میاد و دیگه اصلاً نقطه بعدی بی نقطه بعدی :))
سه:ولی همیشه اوضاع به بدی حالت دوم نیست ممکنه اوضاع مثل حالت اول هم نباشه ممکنه تقریب x1 از تقریب x0 بهتر نباشه ولی به احتمال زیاد اوضاع طوری بشه که آینده روشنی در پیش داشته باشیم.
به شکل زیر دقت کنید:
این حالت همیشه هم بد نیست چون اگه به x1 نگاه کنید با فرض اینکه f تغییر تقعر نده اونوقت می تونید شکل رو 180 درجه تو ذهنتون بچرخونید و ببینید که باز مثله حالتی میشه که تقعر f رو به بالا هست:
به شکل زیر دقت کنید (خودتون ادامه f رو تو ذهنتون ادامه بدید و مکان x2 رو تصور کنید)
شکل زیر دوران شکل بالا هست حتی عبارت y=f(x)x رو هم درست نکردم که قشنگ متوجه این قضیه بشید:))
x0 و x1 که معلومن تو تصویر فکر می کنید x2 کجا باید بیفته؟ (توجه کنید نمودار فوق فقط دوران نمودار f هست و رابطه f رو تغییر ندادیم، فقط برای درک هندسی بهتر داریم نمودار رو می چرخونیم که مطلب جا بیفته)
اصلاً برای اینکه این مورد خوب جا بیفته ما که بیکاریم دوره همی می شینیم یه مثال واقعی رو بررسی می کنیم:
تابع زير رو در نظر بگيريد:
چون مي خواهيم با روش نيوتن رافسون کار کنيم به مشتق اين تابع هم نياز داريم که به صورت زير هست:
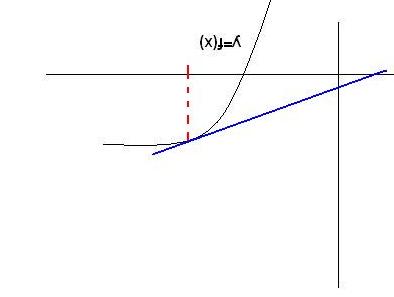
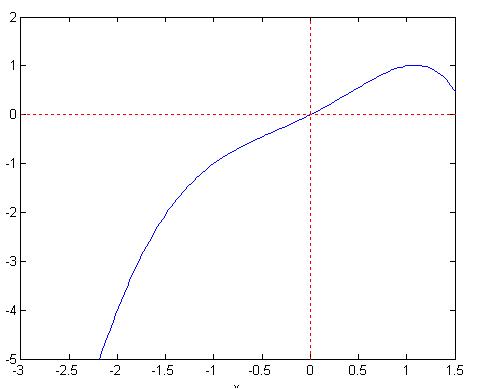
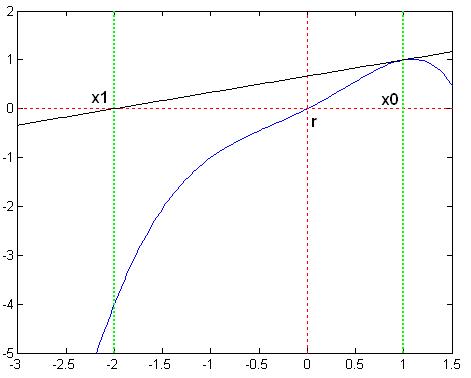
مي خواهيم يه ريشه اين تابع رو تو بازه 3- تا 1.5 پيدا کنيم ( اين ريشه در حقيقت صفر هست) شکل اين تابع توي اين بازه به صورت زيره:
نکته:ممکنه با خودتون بگيد که چرا اينقدر عجيب غريبه اين مثالمون؟ يا من از کجا اينو در آوردم؟؟ اين سوالا سوالات قشنگين که توصيه مي کنم روش فکر کنيد ، چون بعداً چيزاي جالبي در مورد اين سوال ياد خواهيم گرفت:)).
از x0=1 براي تقريب اوليه استفاده مي کنيم.
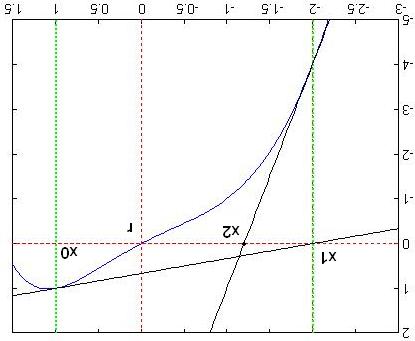
اگه شيب خط مماس توي اين نقطه رو حساب کنيم (خودتون حساب کنيد) ميشه 1/3 ، يعني خط مماس محور x ها رو توي نقطه 2- قطع مي کنه.يا به عبارت ديگه اگه از فرمول نيوتن رافسون استفاده کنيم خواهيم داشت:
(دیگه جایگذاری نقاط توی فرمول با خودتون:دی)
اينم تعبير هندسيش که گيرش هستيم:))
می بینیم که تقعر رو به پایین بوده و در ضمن x1 از x0 بهتر هم نیست ولی اوضاع امیدوار کننده است چرا؟
بزارید x2 رو هم به دست بیاریم:
تعبیر هندسی این موضوع رو هم تو شکل زیر می بینیم:
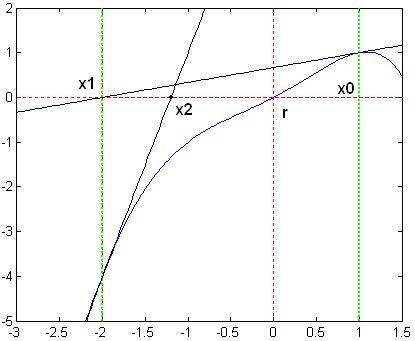
می بینیم که اوضاع داره بهبود پیدا می کنه در حقیقت الآن وضعیت مثل حالتی شده که بالای محور x ها تقعر رو به بالا داشتیم بزارید دوران این شکل رو ببینم تا موضوع معلوم شه:
می بینید؟ معلومه چرا باید x2 بهتر از x1 باشه ، نه؟؟
اینجاست که ممکنه بین علمای بلاد اختلاف پیش بیاد :دی و یه عده خیلی خیلی بچه زرنگ بگن که " خب اگه توی ریشه تغییر تقعر داشته باشیم چی؟"
در جواب باید گفت که این موضوع اوضاع رو از دفعه قبل هم بد تر می کنه
سه حالت ممکنه اتفاق بیفته:
یک: همه چی عادی پیش بره و ریشه به خوبی و خوشی پیدا شه ولی با یه سرعت نسبتاً کمتر
دو:این روش مثل چی بمونه تو گل و هی بین دو تا نقطه دوران کنه و با یه سرعت خیلی خیلی کمتر به جواب برسه
سه:کلاً به جواب نرسه
حالت یک که توضیح نمی خواد ، حالت سه رو به صورت هندسی نشون می دم حالت دو رو هم خودتون تعبیر کنید :))
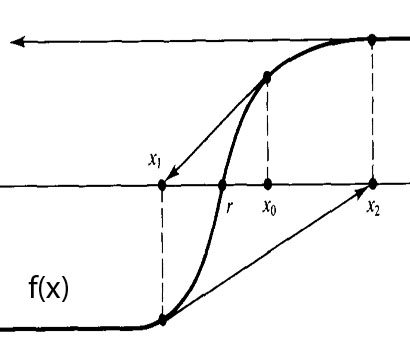
یه توضیح کوچولو هم در مورد حالت دوم بدم ، تو شکل بالا فرض کنید x3 خیلی نزدیک x1 بیفته و x4 هم خیلی نزدیک x2 بیفته و ... (البته دقیقاً تو شکل بالا که نه ، باید یه کم شکل رو تغییر بدید:دی)